Background

In the commutative setting, vector addition over \( \mathbb{Z} \) is straightforward. Given two vectors \( v,w \in \mathbb{Z}^3 \), vector addition is simply defined as addition component-wise. In fact, \( (\mathbb{Z}^3, +) \) actually forms an abelian group, i.e. \( v + w = w + v \). So now consider some basis set of vectors, say \[ S = \{ (0,0,0), (1,0,0), (0,1,0), (0,0,1) \}. \] As an example, we will generate all words of length \( k \). To find these, first take the \( k \)-fold product \( \underbrace{S \times S \times \ldots \times S}_{k \text{ times}} \). Then for each element in \( S \times S \times \ldots \times S \), compute \( s_1 \star s_2 \star \ldots \star s_k \). This will give an element in \( (\mathbb{Z}^3, \star) \). For \( k = 2 \), this yields \[ \begin{align} (0,0,0) + (0,0,0) & = (0,0,0), \\ (0,0,0) + (1,0,0) & = (1,0,0), \\ (0,0,0) + (0,1,0) & = (0,1,0), \\ (0,0,0) + (0,0,1) & = (0,0,1), \\ (1,0,0) + (0,0,0) & = (1,0,0), \\ (1,0,0) + (1,0,0) & = (2,0,0), \\ (1,0,0) + (0,1,0) & = (1,1,0), \\ (1,0,0) + (0,0,1) & = (1,0,1), \\ (0,1,0) + (0,0,0) & = (0,1,0), \\ (0,1,0) + (1,0,0) & = (1,1,0), \\ (0,1,0) + (0,1,0) & = (0,2,0), \\ (0,1,0) + (0,0,1) & = (0,1,1), \\ (0,0,1) + (0,0,0) & = (0,0,1), \\ (0,0,1) + (1,0,0) & = (1,0,1), \\ (0,0,1) + (0,1,0) & = (0,1,1), \\ (0,0,1) + (0,0,1) & = (0,0,2). \end{align} \] Getting rid of duplicates, this yields \[ \begin{align} P_2(S) = \{ & (0,0,0) \\ & (0,0,1) \\ & (0,0,2) \\ & (0,1,0) \\ & (0,1,1) \\ & (0,2,0) \\ & (1,0,0) \\ & (1,0,1) \\ & (1,1,0) \\ & (2,0,0) \}, \end{align} \] where \( P_k(S) \) denotes the polytope generated as the \( k \)th dilate of the basis set \( S \). In other words, \( P_k(S) \) is the set of points realized as words of length \( k \) generated by elements of the basis set \( S \). If we let \( \mathcal{B} \) be an aribitrary (finite) basis set with \( \lvert \mathcal{B} \rvert = n \) and compute the words of length \( k \), then there are \( n(n-1)\ldots(n-k+1) \) evaluations to compute. In this example, the number of points contained in \( P_k(S) \), which we will call the volume, is given by \( V = \binom{k+2}{3} \). Furthermore, it can be seen that there are no "missing spots" in the \( P_k(S) \), so we will say \( P_k(S) \) is saturated if this is the case. Additionally, the outer face of \( P_k(S) \) can be desribed by the function \( z = f(x,y) = k-x-y \). These properties of \( P_k(S) \) motivate the study of polytopes generated in the setting of the Heisenberg group.

---

Setup

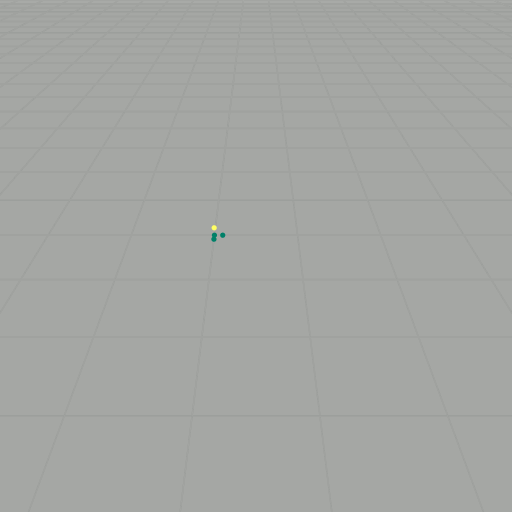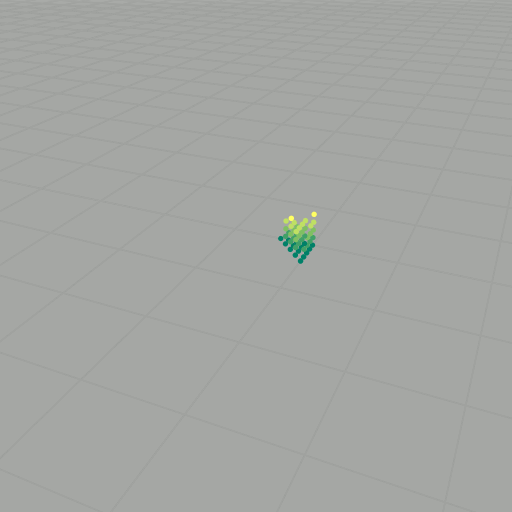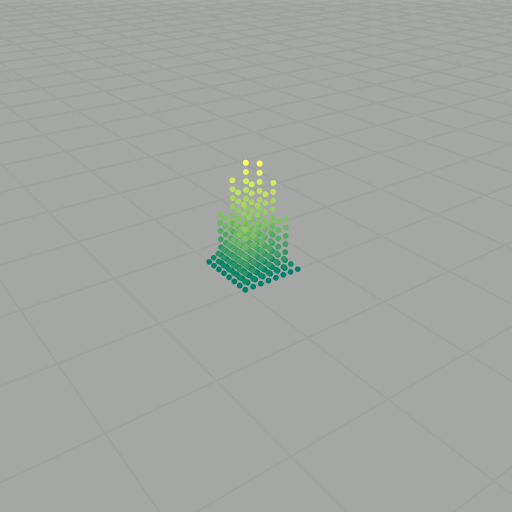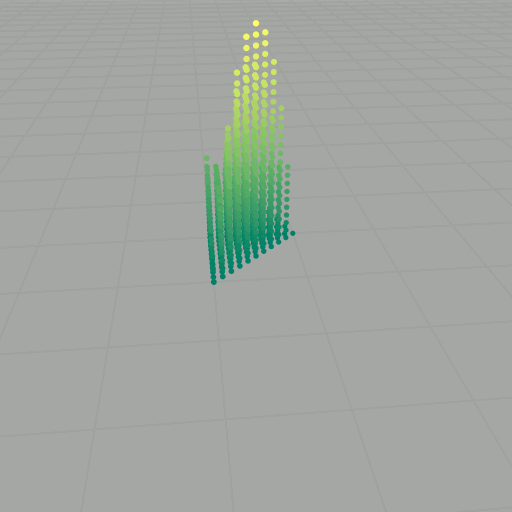
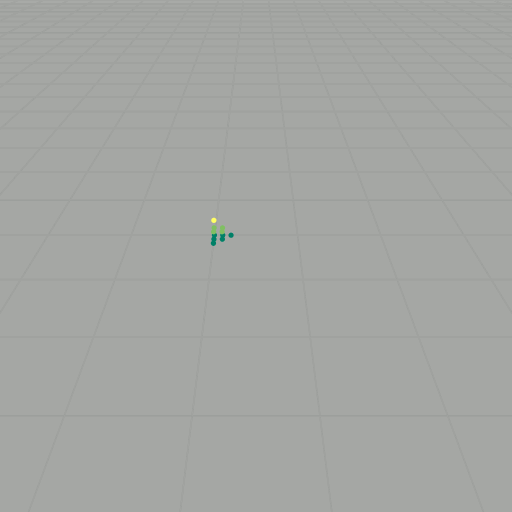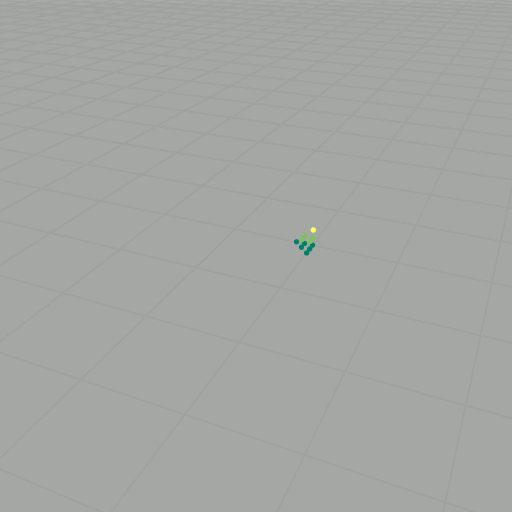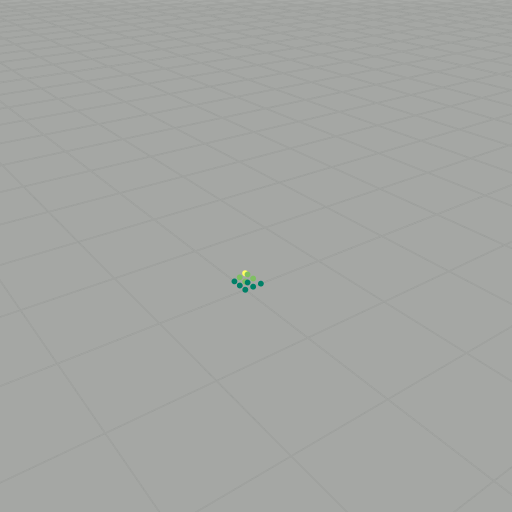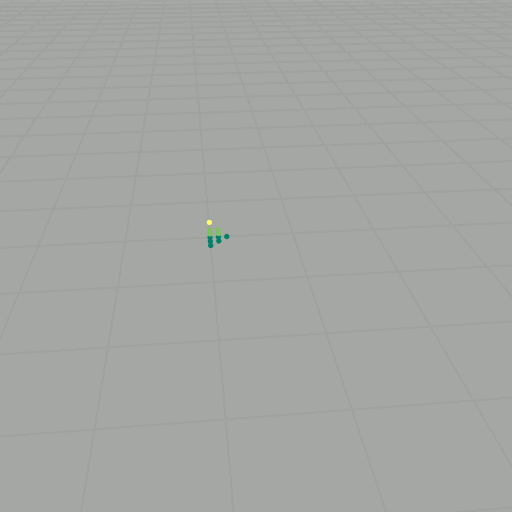
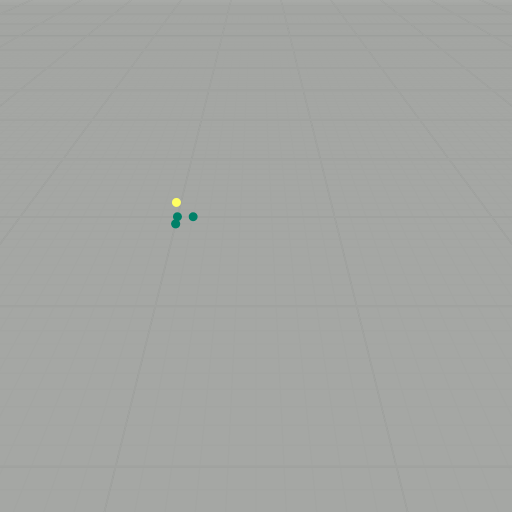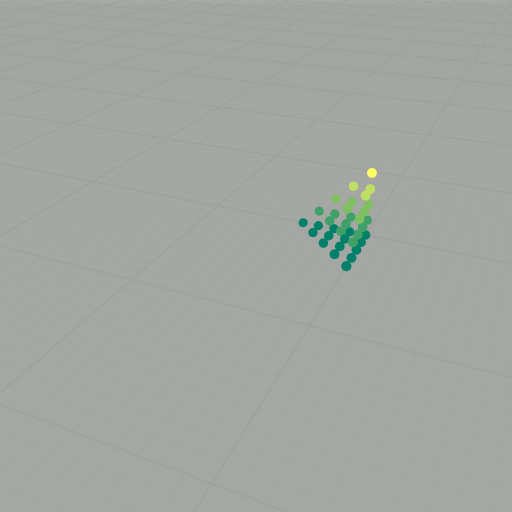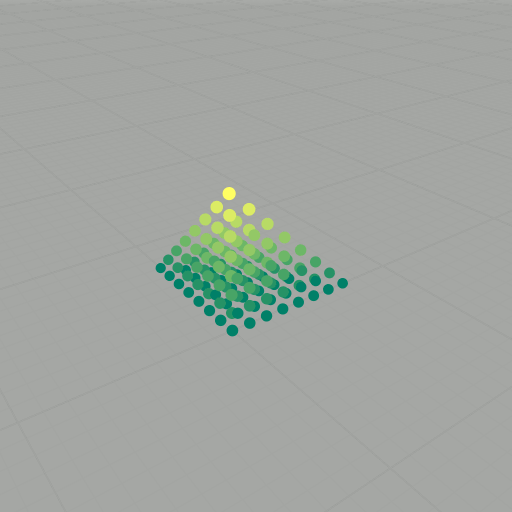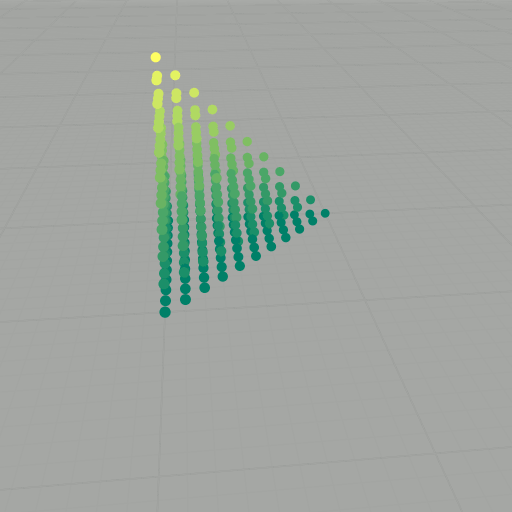
To get to the Heisenberg group, we basically do normal vector addition, but now with a twist: \[ \star \colon \mathbb{Z} \times \mathbb{Z} \longrightarrow \mathbb{Z}, \quad (x, y, z) \star (x', y', z') = (x+x', y+y', z+z'+xy'). \] This new operation is almost normal vector addition, except now there is an extra \( xy' \) tacked onto the \( z \)-component. Because of this new twist, \( (\mathbb{Z}^3, \star) \) forms a noncommutative group. We want to explore this group some more, so now we will consider the we will choose a basis set of vectors, say \( S \) (as we did before). As an example, consider again \( k=2 \): \[ \begin{align} (0,0,0) \star (0,0,0) & = (0,0,0), \\ (0,0,0) \star (1,0,0) & = (1,0,0), \\ (0,0,0) \star (0,1,0) & = (0,1,0), \\ (0,0,0) \star (0,0,1) & = (0,0,1), \\ (1,0,0) \star (0,0,0) & = (1,0,0), \\ (1,0,0) \star (1,0,0) & = (2,0,0), \\ (1,0,0) \star (0,1,0) & = (1,1,1), \\ (1,0,0) \star (0,0,1) & = (1,0,1), \\ (0,1,0) \star (0,0,0) & = (0,1,0), \\ (0,1,0) \star (1,0,0) & = (1,1,0), \\ (0,1,0) \star (0,1,0) & = (0,2,0), \\ (0,1,0) \star (0,0,1) & = (0,1,1), \\ (0,0,1) \star (0,0,0) & = (0,0,1), \\ (0,0,1) \star (1,0,0) & = (1,0,1), \\ (0,0,1) \star (0,1,0) & = (0,1,1), \\ (0,0,1) \star (0,0,1) & = (0,0,2). \end{align} \] Getting rid of duplicates, this yields \[ \begin{align} P_2(S) = \{ & (0,0,0) \\ & (0,0,1) \\ & (0,0,2) \\ & (0,1,0) \\ & (0,1,1) \\ & (0,2,0) \\ & (1,0,0) \\ & (1,0,1) \\ & (1,1,0) \\ & (1,1,1) \\ & (2,0,0) \}, \end{align} \] Since \( (\mathbb{Z}^3, \star) \) is noncommutative, it is important that each word is evaluated according to the order of the elements. We can also visualize these results as points in \( \mathbb{Z}^3 \), as shown in the slideshow below. If we let \( \mathcal{B} \) be an aribitrary (finite) basis set with \( \lvert \mathcal{B} \rvert = n \) and compute the words of length \( k \), then there are \( n^k \) evaluations to compute. For large \( k \), this task becomes intractable.

Results

We can ask the same questions about \( P_k(S) \) as we did in the commutative setting:

• What is the volume of \( P_k(S) \)?
• Is \( P_k(S) \) saturated?
• Can we describe the ceiling function of \( P_k(S) \)?

For this example, since all of the points in \( P-k(S) \) lie in the positive orthant, if we can find a ceiling function of \( P_k(S) \), we can also find the volume by integrating. It turns out that the ceiling function for \( P_k(S) \) is \( z = xy - x - y + k \). So then by integrating with respect to \( x \) and \( y \), we can see that \[ \begin{align*} \lvert P_k(S) \rvert & =\int_{0}^{k} \int_{0}^{k-x} xy - x - y + k \ dy \ dx \\ & =\int_{0}^{k} \int_{0}^{k-x} xy \ dy\ dx + \int_{0}^{k} \int_{0}^{k-x} k - x - y \ dy \ dx \\ & = \int_{0}^{k} \frac{x (k - x)^2}{2} \ dx + \int_{0}^{k} \frac{(k - x)^2}{2} \ dx \\ & = \frac{1}{24} k^4 + \frac{1}{6} k^3 \\ & = \frac{k^4}{4!} + \frac{k^3}{3!}. \end{align*} \]