Problems in Computational Algebraic Geometry¶

Lefschetz properties and toric varieties¶


Sean Grate

March 26th, 2024

Doing research mathematics does not consist solely of ruminating alone in a darkened room, but also of rolling up ones sleeves, writing some code, and having the computer do the legwork.

Overview¶


  • Lefschetz properties
    • Hypersurfaces
    • Betti tables
  • Toric varieties
    • Castelnuovo-Mumford regularity
    • Lattice points and toric surfaces
  • Other projects
    • MatrixSchubert package for Macaulay2
    • Betti numbers of connected sums
    • DBER and course alignment
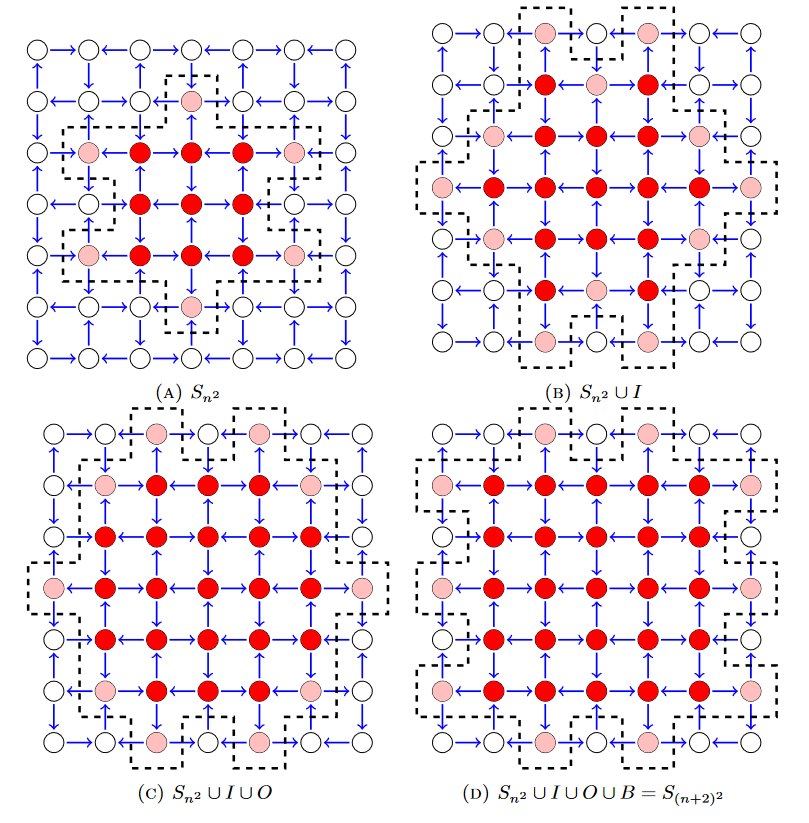
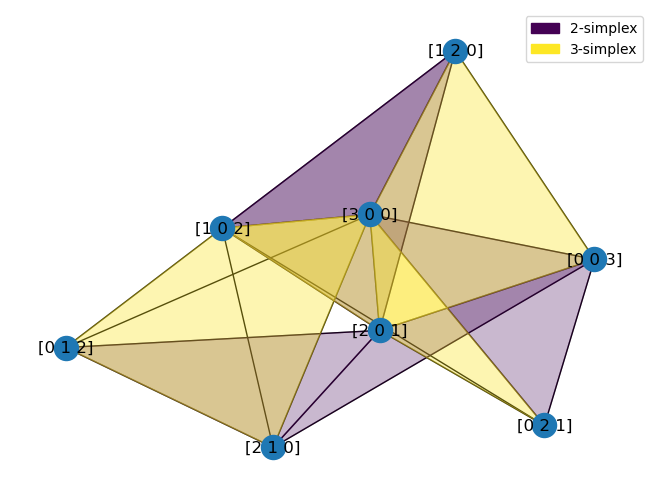
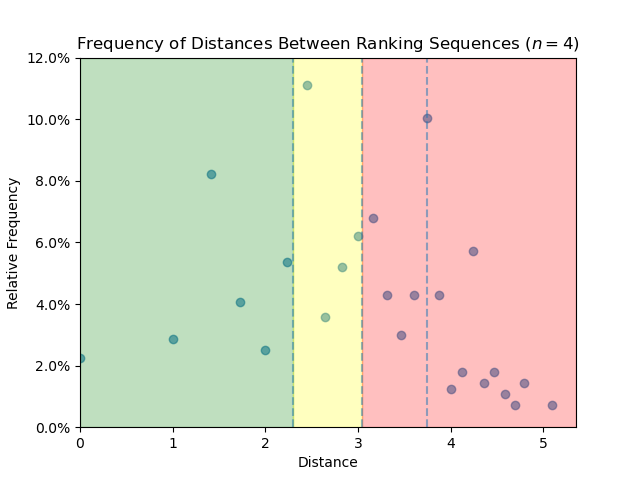
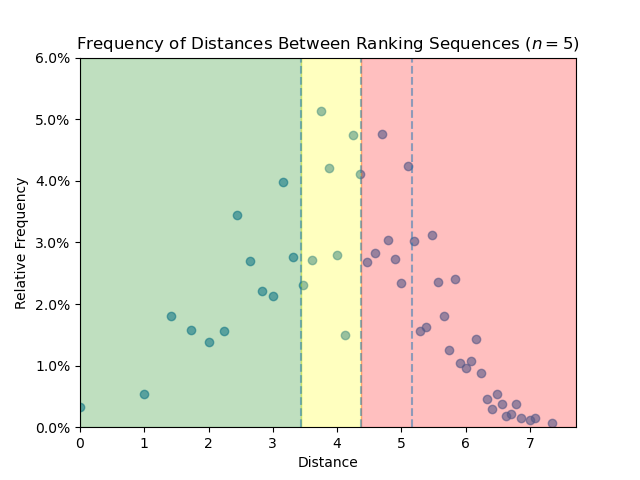
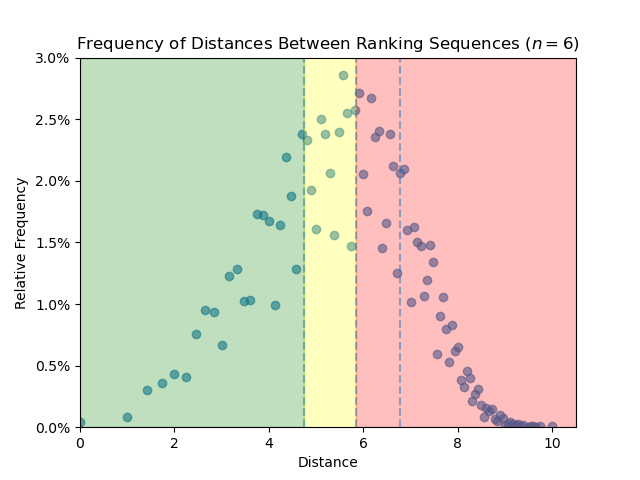
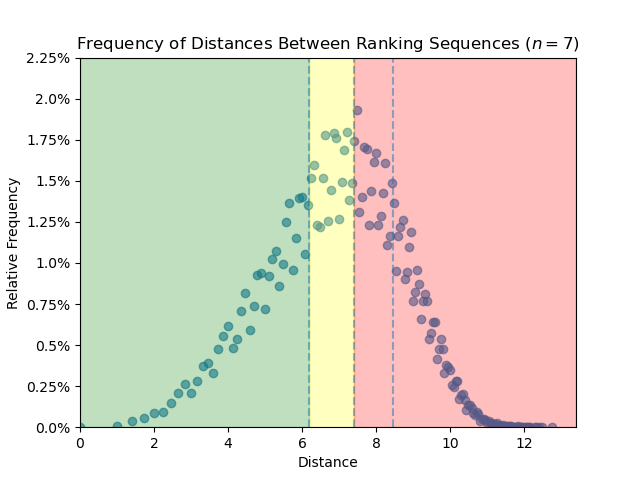
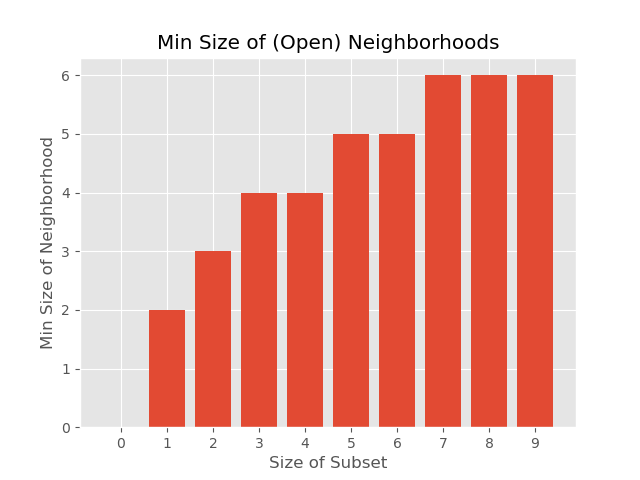
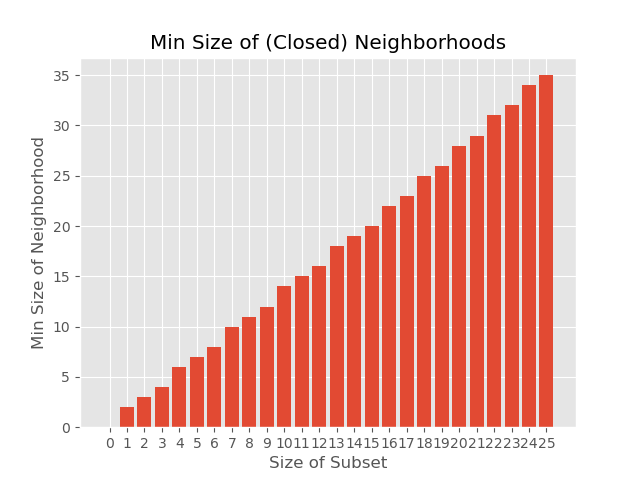
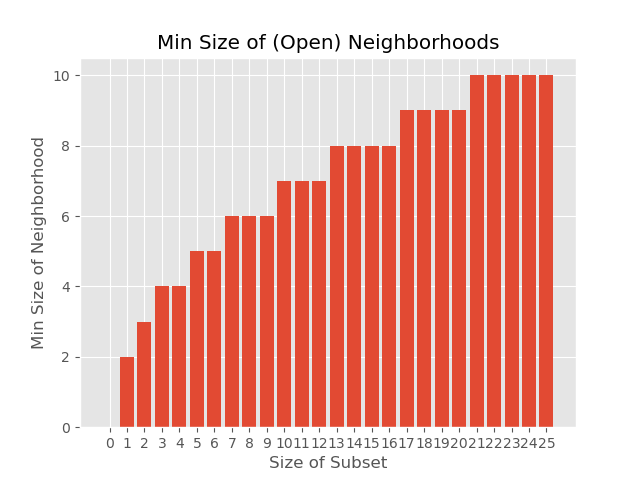
    • Isoperimetry in the $F$-lattice

Lefschetz properties¶

Artinian algebras¶

Definition: A $\mathbb{Z}$-graded $\mathbb{K}$-algebra $A$ is Artinian if $A_d = 0$ for $d \gg 0$.


Example: $A = \mathbb{K}[x,y,z] / \langle x^2,y^2,z^3 \rangle$

$d$ $0$ $1$ $2$ $3$ $4$ $5$
$\text{gens}(A_d)$ $1$ $x$
$y$
$z$		 $xy$
$xz$
$yz$
$z^2$		 $xyz$
$xz^2$
$yz^2$		 $xyz^2$ $\emptyset$
$\text{dim}(A_d)$ $1$ $3$ $4$ $3$ $1$ $0$

Example: If $I_\Delta \subseteq \mathbb{K}[x_1,\dots,x_n]$ is a Stanley-Reisner ideal, then $I_\Delta + \langle x_i^2 \, | \, 1 \leq i \leq n \rangle$ is Artinian.

In [8]:
kk = ZZ/32749
R = kk[x,y,z]
I = ideal(x^2, y^2, z^3)
A = R/I

-- why do by hand what you can do by computer...?
ds = {"d"} | for i in 0..5 list i
mons = {"gens(A_d)"} | for i in 0..5 list netList(flatten entries basis(i, A), Boxes=>false)
dims = {"dim(A_d)"} | for i in 0..5 list hilbertFunction(i, A)
print netList({ds} | {mons} | {dims}, HorizontalSpace=>2, VerticalSpace=>1, Alignment=>Center)

+-------------+-----+-----+-------+---------+----------+-----+
|             |     |     |       |         |          |     |
|      d      |  0  |  1  |   2   |    3    |     4    |  5  |
|             |     |     |       |         |          |     |
+-------------+-----+-----+-------+---------+----------+-----+
|             |     |     |       |         |          |     |
|             |     |     |       |         |       2  |     |
|  gens(A_d)  |  1  |  x  |  x*y  |  x*y*z  |  x*y*z   |     |
|             |     |  y  |  x*z  |     2   |          |     |
|             |     |  z  |  y*z  |  x*z    |          |     |
|             |     |     |   2   |     2   |          |     |
|             |     |     |  z    |  y*z    |          |     |
|             |     |     |       |         |          |     |
+-------------+-----+-----+-------+---------+----------+-----+
|             |     |     |       |         |          |     |
|   dim(A_d)  |  1  |  3  |   4   |    3    |     1    |  0  |
|             |     |     |       |         |          |     |
+-------------+-----+-----+-------+---------+----------+-----+
In [9]:
-- Artinian => Hilbert series is a polynomial
print("Hilbert series: " | toString(hilbertSeries(A, Reduce=>true)))

Hilbert series: (1+3*T+4*T^2+3*T^3+T^4)/(1)
In [10]:
-- Artinian <=> Krull dim = 0
print("R/I = " | toString(describe(A)) | 
      " is Artinian: " | toString(dim(A) == 0))

R/I = R/(x^2,y^2,z^3) is Artinian: true

Weak Lefschetz property (WLP)¶


For all $f \in A$, $f$ is a zero-divisor. The best we can hope for is $\exists \, f \in A$ such that $\cdot f$ is injective or surjective in all degrees.

Definition: $A = R/I$ has the weak Lefschetz property (WLP) if $A_i \xrightarrow{\cdot l} A_{i+1}$ is full rank (i.e., either injective or surjective) for all $i \geq 0$.

Who cares?¶


  • Geometric combinatorics

    • $g$-theorem (formerly McMullen's conjecture)
    • log-concavity of sequences (e.g., $f$-vectors)
    • top-heavy theorem (easy* way of getting a Field's medal)

  • Commutative algebra

    • Fröberg's conjecture
    • Growth of Hilbert functions

WLP is hard¶


Theorem [Brenner, Kaid; 2010]

Let $\text{char}(\mathbb{K}) = 2$. Then $A = \mathbb{K}[x,y,z] / \langle x^d, y^d, z^d \rangle$ has the WLP if and only if $d = \left\lfloor \frac{2^k + 1}{3} \right\rfloor$ for some positive integer $k$.


Theorem [Harbourne, Schenck, Seceleanu; 2011]

Let $$ I = \langle L_1^t, \dots, L_n^t \rangle \subset \mathbb{K}[x_1,x_2,x_3,x_4] $$ with $L_i \in R_1$ generic. If $n \in \{5,6,7,8\}$, then the WLP fails, respectively, for $t \geq \{3,27,140,704\}$.


Question

Does every complete intersection in four or more variables have the WLP?

Start with geometry¶

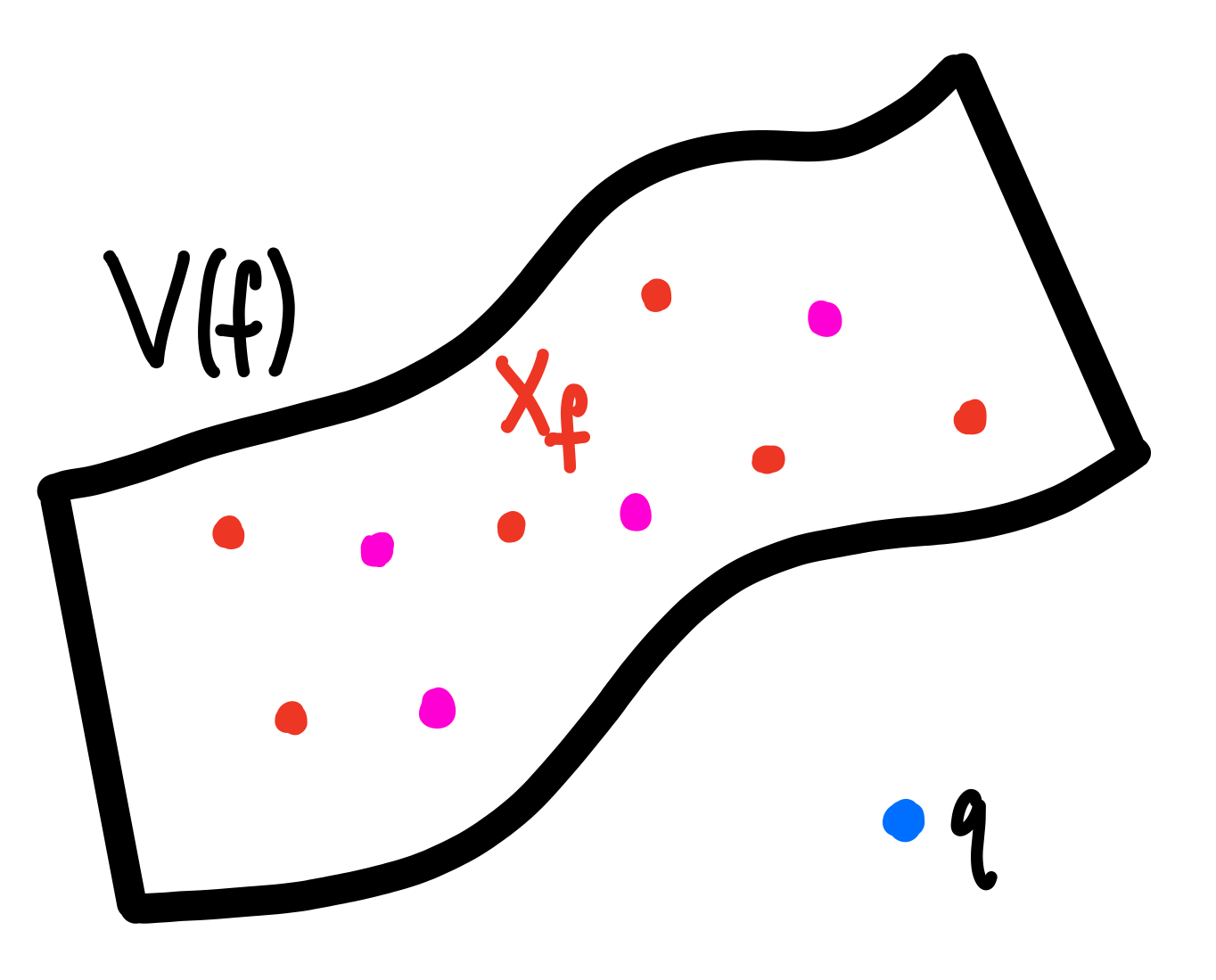
Theorem [G., Schenck]: Let $X_f \subset \mathbb{P}^n$ be a set of distinct points lying on a distinct points lying on a unique hypersurface $\mathbf{V}(f)$ with $\text{deg}(f) = d$ such that $\mathbf{I}(X_f) = (f)$. Choose $q \not\in \mathbf{V}(f)$ such that if $X = X_f \cup \{f\}$, then $$\mathbf{I}(X)_d = 0 \quad \text{and} \quad \text{dim}_{\mathbb{K}}(\mathbf{I}(X)_{d+1}) = n.$$ Then the Artinian reduction $A_X$ does not have the WLP. In particular, if $I$ is a general linear form, then $A_d \xrightarrow{\cdot l} A_{d+1}$ does not have full rank.

hypersurface

Betti tables¶

Given an ideal $I \subset \mathbb{K}[x_1,\dots,x_n]$, a (minimal) free resolution "approximates" $R/I$. The betti table records the ranks of the summands appearing in the free resolution.

Example: $R = \mathbb{K}[x,y,z]$ and $I = \langle x^2, y^2, z^3 \rangle$ $$0 \leftarrow R/I \leftarrow R \leftarrow \substack{R(-2)^2 \\ \oplus \\ R(-3)} \leftarrow \substack{R(-4) \\ \oplus \\ R(-5)^2} \leftarrow R(-7) \leftarrow 0$$

In [12]:
F = res I

-- resolution and summands
print F

 1      3      3      1
R  <-- R  <-- R  <-- R  <-- 0
                             
0      1      2      3      4
In [13]:
-- differentials in the complex
print F.dd

     1                    3
0 : R  <---------------- R  : 1
          | x2 y2 z3 |

     3                           3
1 : R  <----------------------- R  : 2
          {2} | -y2 -z3 0   |
          {2} | x2  0   -z3 |
          {3} | 0   x2  y2  |

     3                   1
2 : R  <--------------- R  : 3
          {4} | z3  |
          {5} | -y2 |
          {5} | x2  |

     1
3 : R  <----- 0 : 4
          0
In [17]:
-- summands in free resolution
for i in 0..length(F) do print(toString(i) | ": " | toString flatten degrees F_i)

-- Betti table
print betti F

-- invariants from Betti table
print("Projective dimension of R/I: " | toString pdim (R^1/I))
print("Regularity of R/I: " | toString regularity(R^1/I))

0: {0}
1: {2, 2, 3}
2: {4, 5, 5}
3: {7}

       0 1 2 3
total: 1 3 3 1
    0: 1 . . .
    1: . 2 . .
    2: . 1 1 .
    3: . . 2 .
    4: . . . 1

Projective dimension of R/I: 3

Regularity of R/I: 4

Koszul tails¶


Definition: A Betti table $B$ has an $(n,d)$-Koszul tail if it has an upper-left principal block of the form $$ \begin{array}{c|ccccccccc} & 0 & 1 & 2 & 3 & \dots & n-2 & n-1 & n & n+1 \\ \hline 0 & 1 & . & . & . & \dots & . & . & . & * \\ 1 & . & . & . & . & \dots & . & . & . & * \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & * \\ d-1 & . & . & . & . & \dots & . & . & . & * \\ d & . & n & \binom{n}{2} & \binom{n}{3} & \dots & \binom{n}{n-2} & n & 1 & * \\ d+1 & * & * & * & * & * & * & * & * & * \end{array}. $$ If $B$ is has an $(n,d)$-Koszul tail and is the Betti table for an Artinian ring $\mathbb{K}[x_1,\dots,x_n]/I$, then we say $B$ has a maximal $(n,d)$-Koszul tail.

Koszul tails¶

In [21]:
kk = ZZ/32749
R = kk[x_1..x_4]
allPoints = transpose matrix{{1,0,0,0},{0,1,0,0},{1,1,1,0},{0,0,1,0},{0,1,1,0},{1,1,0,0},{1,0,1,0},{0,0,0,1}}**kk

-- compute the Artinian reduction
Ired = Ared sub(pointsIdeal allPoints, R)
print allPoints
print minimalBetti ideal Ired
print("Has WLP: " | toString(checkWLP ideal Ired))

| 1 0 1 0 0 1 1 0 |
| 0 1 1 0 1 1 0 0 |
| 0 0 1 1 1 0 1 0 |
| 0 0 0 0 0 0 0 1 |

       0 1 2 3
total: 1 6 8 3
    0: 1 . . .
    1: . 3 3 1
    2: . 3 4 1
    3: . . 1 1

Has WLP: false

Results¶

Theorem [G., Schenck; 2023]

An Artinian algebra $A = \mathbb{K}[x_1,\dots,x_n]/I$ whose Betti table has a maximal $(n,d)$-Koszul tail does not have the WLP.

Corollary

If $T = \mathbb{K}[x_1,\dots,x_n]/I$ is Cohen-Macaulay of dimension $m$, and the Betti table of $T$ has a maximal $(n-m,d)$-Koszul tail, then the Artinian reduction of $T$ does not have the WLP.

Corollary

If $A = \mathbb{K}[x_1,\dots,x_{m+n}]/I$ is Artinian with an $(n,d)$-Koszul tail, and there exists a sequence of linearly independent linear forms $\{l_1,\dots,l_m\}$ such that the Betti tables of $A$ and $A/I_L$ have the same top row, then $A/I_L$ does not have the WLP.

Future work¶

  • Can we do better than a Koszul tail? Having a Koszul tail is very strict.
  • Is there a "nice" Boij-Söderberg theory underlying this?
  • Characterize the Stanley-Reisner rings whose Artinian reductions have a Koszul tail.

Toric Varieties¶

Lattice points¶

A set of lattice points, represented as the columns of the $d \times n$ matrix defines a map of monomials.

Example

$$ A = \begin{pmatrix} d & d-1 & \dots & 1 & 0 \\ 0 & 1 & \dots & d-1 & d \end{pmatrix} $$

$A$ consists of the integral points on the line $x+y=d$ with $x,y \geq 0$. It defines the monomial curve $C$ given as the image of the map

$$(s,t) \longmapsto (s^d, s^{d-1} t, \dots, s t^{d-1}, t^d).$$

The kernel of this map defines the toric ideal $I_C$.

Example: twisted cubic¶

$$A = \begin{pmatrix} 3 & 2 & 1 & 0 \\ 0 & 1 & 2 & 3 \end{pmatrix}$$

The monomial curve $C$ is the image of the map $(s,t) \mapsto (s^3, s^2 t, s t^2, t^3)$. Set $$x_0 = s^3, \quad x_1 = s^2 t, \quad x_2 = s t^2, \quad x_3 = t^3.$$ Then $$I_C = \langle x_1 x_2 - x_0 x_3, x_1^2 - x_0 x_2, x_2^2 - x_1 x_3 \rangle.$$

In [12]:
-- twisted cubic
kk = ZZ/32749
R = kk[x_0..x_3]
I = monomialCurveIdeal(R, {1,2,3})

print I
print betti res I

        2                       2
ideal (x  - x x , x x  - x x , x  - x x )
        2    1 3   1 2    0 3   1    0 2

       0 1 2
total: 1 3 2
    0: 1 . .
    1: . 3 2

Castelnuovo-Mumford regularity¶

Definition: Let $I \subseteq R = \mathbb{K}[x_0,\dots,x_n]$ be a homogeneous ideal, and consider the minimal free resolution $$0 \leftarrow R/I \leftarrow F_0 \leftarrow \dots \leftarrow F_{n+1} \leftarrow 0$$ of $R/I$, where $F_i \cong \bigoplus_j R(-i-j)^{\beta_{i,j}}$. The Castelnuovo-Mumford regularity (or simply regularity) is $$\text{reg}(R/I) = \max_{i,j} \left\{ j \, \colon \, \beta_{i,j} \neq 0 \right\}.$$

Note: The regularity is the index of the bottom row in the Betti table.

Regularity of monomial curves¶

Theorem [L'vovsky; 1996]: Let $A = (0,a_1,\dots,a_n)$ be a sequence of non-negative integers such that the g.c.d. of the $a_j$'s equals $1$, and let $C$ be the corresponding monomial curve. Then $C$ is $\delta$-regular, where $$\delta = \max_{1 \leq i < j \leq n} \{ (a_i - a_{i-1}) + (a_j - a_{j-1}) \},$$ i.e., $\delta$ is the sum of the two largest gaps in the semigroup generated by $A$.

In [18]:
-- twisted cubic
I = monomialCurveIdeal(kk[x_0..x_3], {1,2,3})
print betti res I
print(toString I | " -> reg(I) = " | toString regularity I)

-- sporadic
I = monomialCurveIdeal(kk[x_0..x_4], {1,2,3,5})
print betti res I
print(toString I | " -> reg(I) = " | toString regularity I)

       0 1 2
total: 1 3 2
    0: 1 . .
    1: . 3 2

ideal(x_2^2-x_1*x_3,x_1*x_2-x_0*x_3,x_1^2-x_0*x_2) -> reg(I) = 2

       0 1 2 3
total: 1 5 5 1
    0: 1 . . .
    1: . 5 5 .
    2: . . . 1

ideal(x_3^2-x_1*x_4,x_2*x_3-x_0*x_4,x_2^2-x_1*x_3,x_1*x_2-x_0*x_3,x_1^2-x_0*x_2) -> reg(I) = 3

Regularity of toric surfaces¶

Now working with lattice points in the plane (and then homogenizing).

Examples

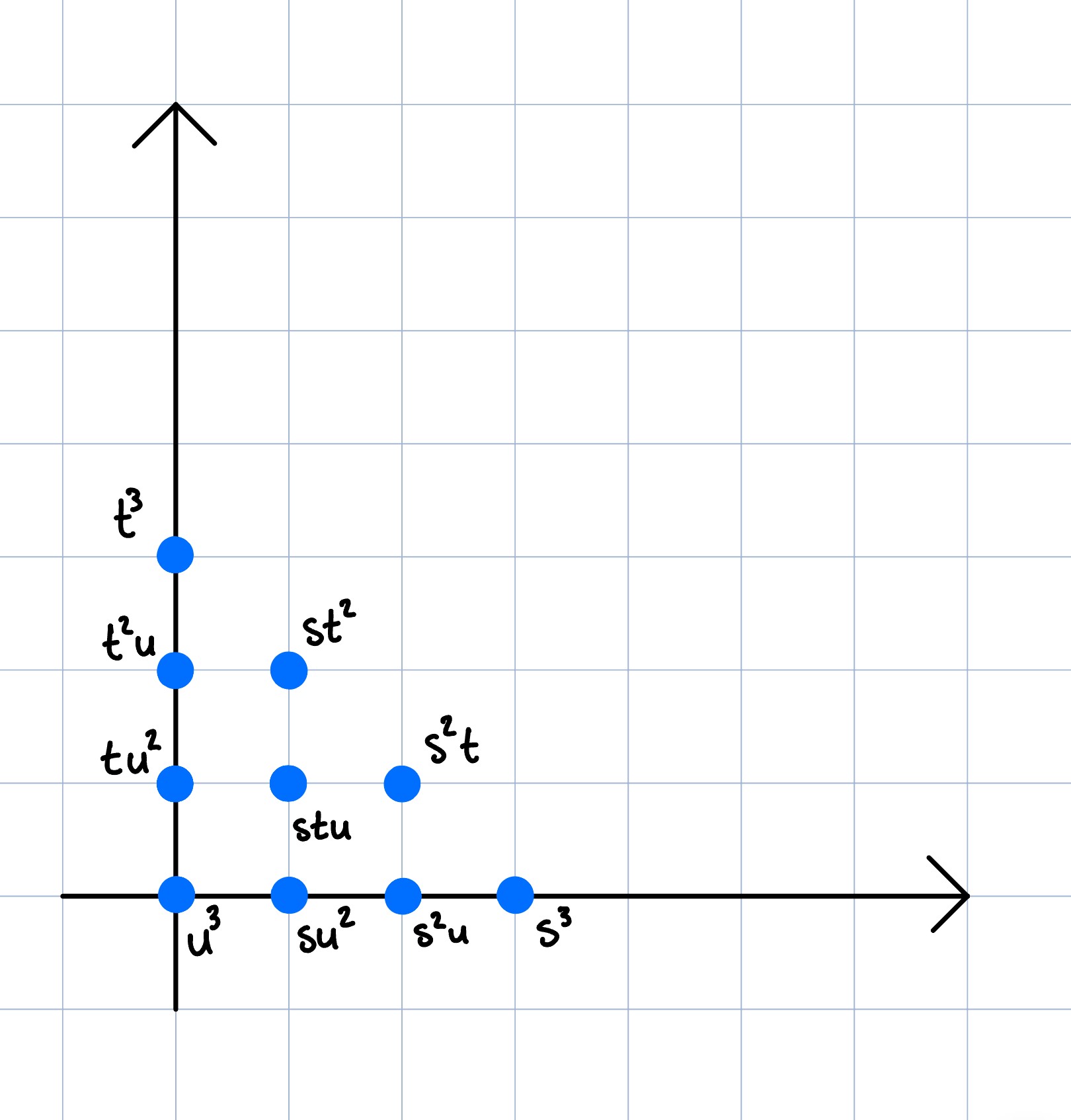
full_triangle
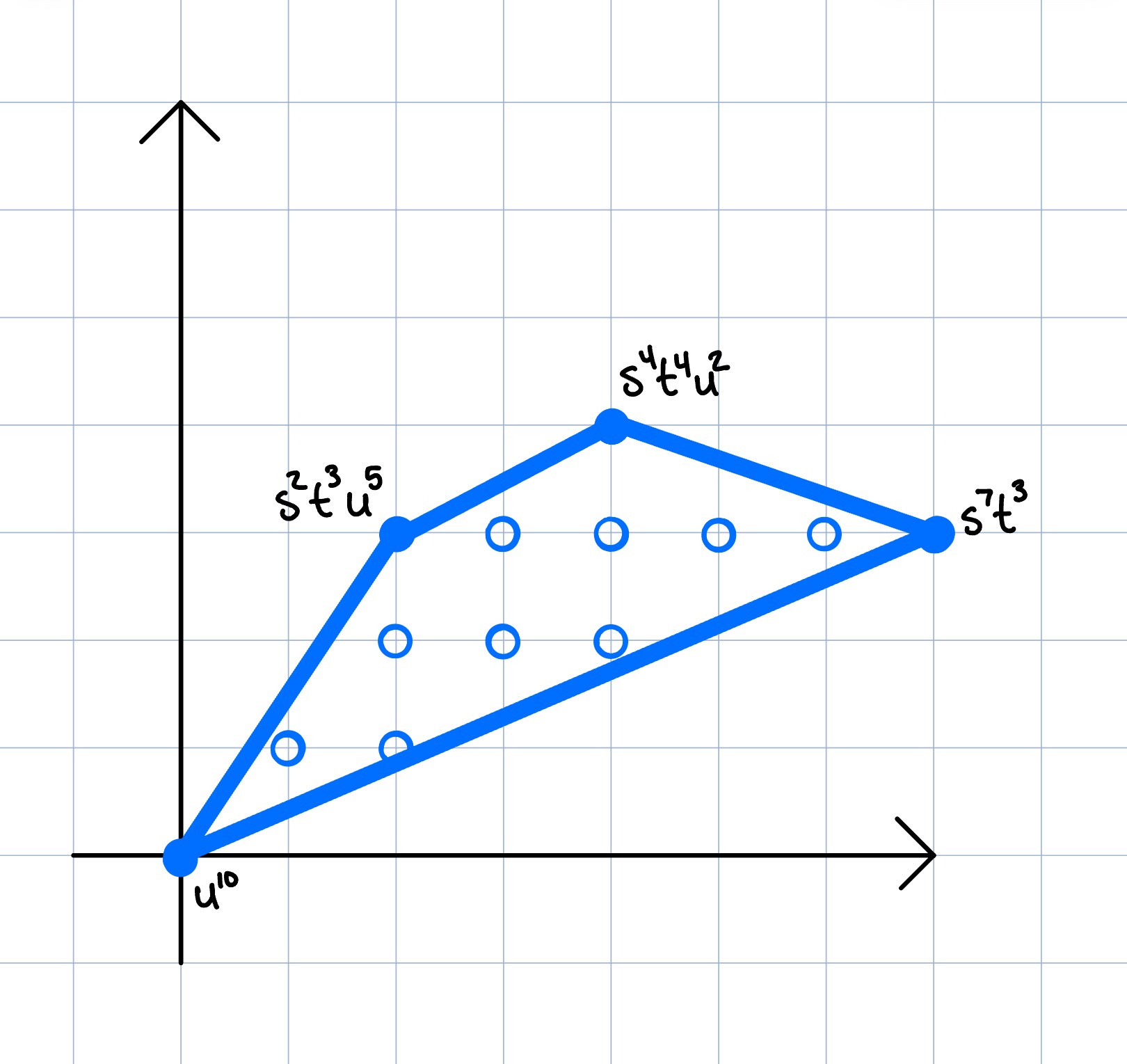
bad_boy
In [22]:
-- Veronese
A = homogenizeLatticePoints transpose matrix {{0,0},{1,0},{2,0},{3,0},{0,1},{1,1},{2,1},{0,2},{1,2},{0,3}}
I = latticeIdeal A

print A
print minimalBetti I

| 0 1 2 3 0 1 2 0 1 0 |
| 0 0 0 0 1 1 1 2 2 3 |
| 3 2 1 0 2 1 0 1 0 0 |

       0  1   2   3   4   5  6 7
total: 1 27 105 189 189 105 27 1
    0: 1  .   .   .   .   .  . .
    1: . 27 105 189 189 105 27 .
    2: .  .   .   .   .   .  . 1
In [26]:
-- badBoy example from Hal
A = transpose matrix{{0,0},{7,3},{4,4},{2,3}}
I = latticeIdeal homogenizeLatticePoints A

print I
print betti res I   -- regularity = 19

       5 15    4 16
ideal(x x   - x x  )
       0 2     1 3

       0 1
total: 1 1
    0: 1 .
    1: . .
    2: . .
    3: . .
    4: . .
    5: . .
    6: . .
    7: . .
    8: . .
    9: . .
   10: . .
   11: . .
   12: . .
   13: . .
   14: . .
   15: . .
   16: . .
   17: . .
   18: . .
   19: . 1

Hollow regular polygons¶

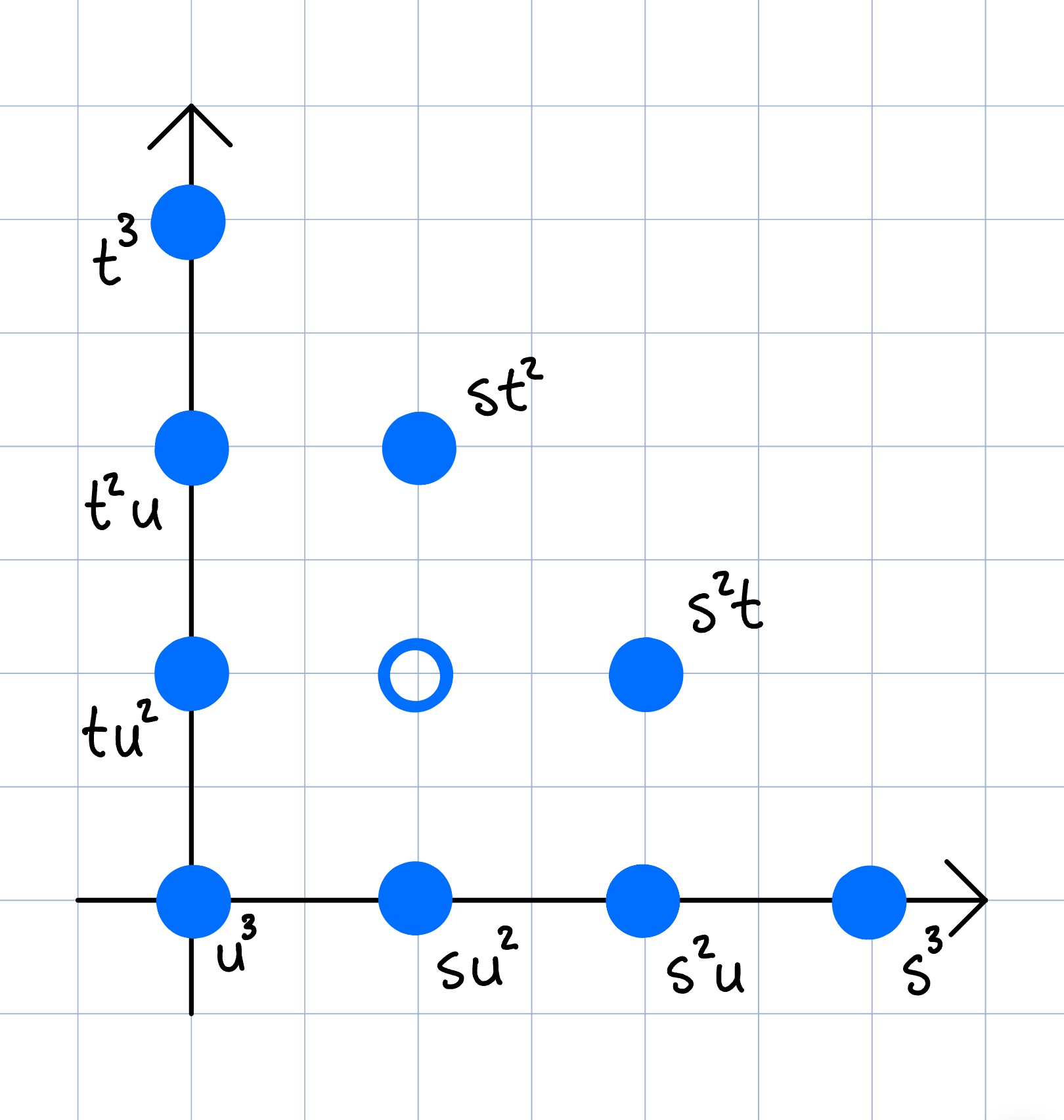
triangle3
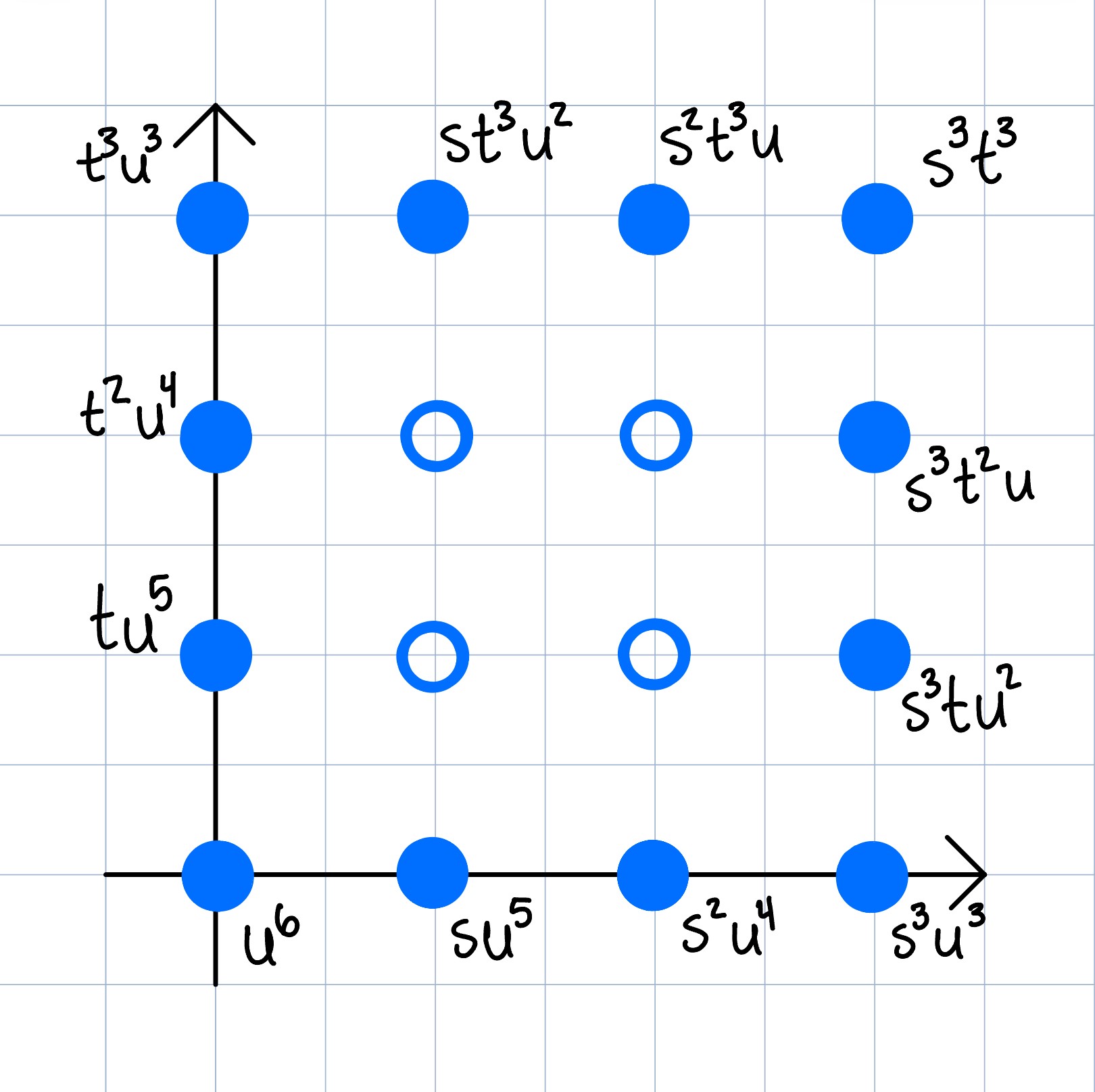
square3
In [27]:
-- hollow triangles of lengths 2, 3, and 4
for k from 2 to 4 do (
    A = hollowPolygon homogenizeLatticePoints transpose matrix{{0,0},{k,0},{0,k}};
    print minimalBetti(latticeIdeal A);
    print "\n"
)

       0 1 2 3
total: 1 6 8 3
    0: 1 . . .
    1: . 6 8 3


       0  1  2  3   4  5  6 7 8
total: 1 17 53 91 108 83 37 9 1
    0: 1  .  .  .   .  .  . . .
    1: . 17 43 36   8  .  . . .
    2: .  . 10 55 100 83 37 9 1


       0  1   2   3    4    5    6    7   8   9 10 11
total: 1 33 153 525 1356 2178 2205 1486 675 201 36  3
    0: 1  .   .   .    .    .    .    .   .   .  .  .
    1: . 33 123 144   30    .    .    .   .   .  .  .
    2: .  .  30 381 1326 2178 2205 1486 675 201 36  3
In [28]:
-- hollow squares of lengths 2, 3
for k from 2 to 4 do (
    A = hollowPolygon homogenizeLatticePoints transpose matrix{{0,0},{k,0},{0,k},{k,k}};
    print minimalBetti(latticeIdeal A);
    print "\n"
)

       0  1  2  3  4  5 6 7
total: 1 11 34 57 55 29 8 1
    0: 1  .  .  .  .  . . .
    1: . 11 17  6  .  . . .
    2: .  . 17 51 55 29 8 1


       0  1   2   3    4    5    6    7   8   9 10 11
total: 1 29 232 942 2176 3154 3045 2008 903 268 48  4
    0: 1  .   .   .    .    .    .    .   .   .  .  .
    1: . 29  84  90   48   10    .    .   .   .  .  .
    2: .  . 148 852 2128 3144 3045 2008 903 268 48  4



o28 = [KERNEL ENFORCED TIMEOUT]

Preliminary work¶

Conjecture: $\text{reg}(\triangle^k) = 2$ for all $k \geq 3$.

Conjecture: Let $P_d^k$ be a regular $d$-gon with integral boundary points and side length $k$. Then $\text{reg}(P_d^k) = 2$ for all $k \geq 3$.

Tools (Hochster's formula)¶

Theorem (Hochster's formula): Given a set of lattice points $A$, let $\mathcal{A}$ be the semigroup determined by $A$ and $I$ its lattice ideal. Define $$\Delta_{\mathbf{b}} = \left\{ I \subseteq [n] \, \colon \, \mathbf{b} - \sum_{i \in I} \mathbf{a}_i \in \mathcal{A} \right\}.$$ Then $$\beta_{i, \mathbf{b}}(I) = \dim_{\mathbb{K}} \tilde{H}_i(\Delta_{\mathbf{b}}, \mathbb{K}).$$

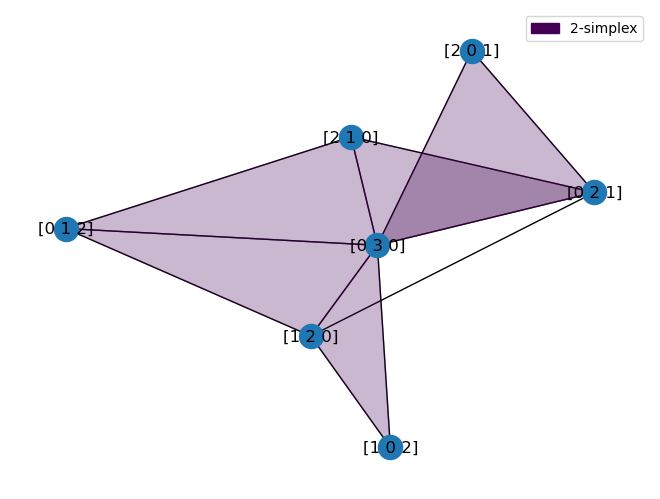
Example $$A = \triangle^3 = \begin{pmatrix} 3 & 2 & 1 & 0 & 2 & 0 & 1 & 0 & 0 \\ 0 & 1 & 2 & 3 & 0 & 2 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 2 & 2 & 0 \end{pmatrix} $$

Example (cont.)

# left image
Multidegree: [2 8 2]
Homogeneous degree: 4
Reduced betti numbers: (0, 1, 0)
f-vector: (1, 7, 12, 5)

# right image
Multidegree: [6 2 4]
Homogeneous degree: 4
Reduced betti numbers: (0, 1, 1, 0)
f-vector: (1, 8, 21, 17, 3)
hochster1
hochster2

Tools (sheaf cohomology)¶

  • Short exact sequence of sheaves induces a long exact sequence in sheaf cohomology
  • Sheaf cohomology is related to lattice points (in our case)
  • Sheaf cohomology $\leftrightarrow$ regularity
  • Show certain sheaf cohomology vanishes $\implies$ regularity is small

Other Projects¶

MatrixSchubert package for Macaulay2¶

pipe_dream

Joint with Ayah Almousa, Daoji Huang, Patricia Klein, Adam LaClair, Yuyuan Luo, Joseph McDonough

Betti numbers of connected sums¶

Joint with Nasrin Altafi, Roberta Di Gennaro, Federico Galetto, Rosa M. Mirò-Roig, Uwe Nagel, Alexandra Seceleanu, Junzo Watanabe

DBER and course alignment¶

Joint with Haile Gilroy and Melinda Lanius

align4
align5
align6
align7

Isoperimetry in the $F$-lattice¶

f-lattice
minimizers

Joint with Nicholas Gaubatz and Haile Gilroy

closed1
closed2
closed1
closed2

Summary¶

Completed¶

Betti tables forcing failure of the Weak Lefschetz Property (published)

Betti numbers for connected sums of graded Gorenstein artinian algebras (submitted)

| The MatrixSchubert package for Macaulay2 (submitted)

Suturing the Severed Didactic Tetrahedron: Graph Theoretic Reflection to Foster Alignment in Coordinated Course (submitted)

On the docket¶

Castelnuovo-Mumford regularity of toric surfaces

Minimal Sizes of out-neighborhoods in the $F$-lattice (in preparation)

Stanley-Reisner rings failing the Weak Lefschetz Property

Using topological data analysis as a classification tool

The cone of Koszul tails