Castelnuovo-Mumford regularity¶
Definition: Let $I \subseteq R = \mathbb{K}[x_0,\dots,x_n]$ be a homogeneous ideal, and consider the minimal free resolution $$0 \leftarrow R/I \leftarrow F_0 \leftarrow \dots \leftarrow F_{n+1} \leftarrow 0$$ of $R/I$, where $F_i \cong \bigoplus_j R(-i-j)^{\beta_{i,j}}$. The Castelnuovo-Mumford regularity (or simply regularity) is $$\text{reg}(R/I) = \max_{i,j} \left\{ j \, \colon \, \beta_{i,j} \neq 0 \right\}.$$
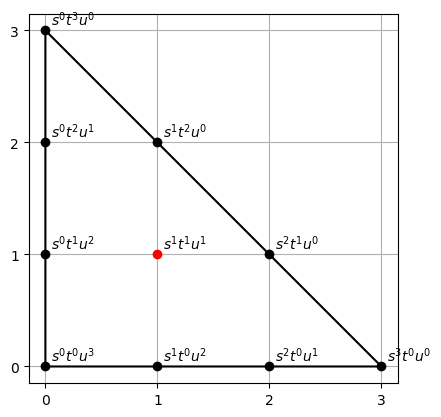
Note: The regularity is the index of the bottom row in the Betti table.
Regularity of monomial curves¶
Theorem [L'vovsky; 1996]: Let $A = (0,a_1,\dots,a_n)$ be a sequence of non-negative integers such that the g.c.d. of the $a_j$'s equals $1$, and let $C$ be the corresponding monomial curve. Then $C$ is $\delta$-regular, where $$\delta = \max_{1 \leq i < j \leq n} \{ (a_i - a_{i-1}) + (a_j - a_{j-1}) \},$$ i.e., $\delta$ is the sum of the two largest gaps in the semigroup generated by $A$.
kk = ZZ/32749
-- twisted cubic
I = monomialCurveIdeal(kk[x_0..x_3], {1,2,3})
print betti res I
print(toString I | " -> reg(I) = " | toString regularity I)
-- sporadic
I = monomialCurveIdeal(kk[x_0..x_3], {3,5,7})
print betti res I
print(toString I | " -> reg(I) = " | toString regularity I)
0 1 2
total: 1 3 2
0: 1 . .
1: . 3 2
ideal(x_2^2-x_1*x_3,x_1*x_2-x_0*x_3,x_1^2-x_0*x_2) -> reg(I) = 2
0 1 2
total: 1 3 2
0: 1 . .
1: . 1 .
2: . . .
3: . 2 2
ideal(x_2^2-x_1*x_3,x_1^3*x_2-x_0^2*x_3^2,x_1^4-x_0^2*x_2*x_3) -> reg(I) = 4
-- pinched Veronese
A = homogenizeLatticePoints hollowPolygon transpose matrix {{0,0}, {3,0}, {0,3}}
I = latticeIdeal A
print A
print minimalBetti I
| 0 1 2 3 0 2 0 1 0 |
| 0 0 0 0 1 1 2 2 3 |
| 3 2 1 0 2 0 1 0 0 |
0 1 2 3 4 5 6 7 8
total: 1 17 53 91 108 83 37 9 1
0: 1 . . . . . . . .
1: . 17 43 36 8 . . . .
2: . . 10 55 100 83 37 9 1
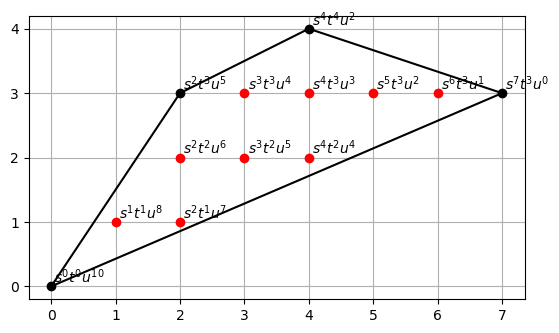
-- bad boy example from Hal
A = transpose matrix {{0,0}, {7,3}, {4,4}, {2,3}}
I = latticeIdeal homogenizeLatticePoints hollowPolygon A
print I
print betti res I -- regularity = 19
16 4 5 15
ideal(x x - x x )
1 2 0 3
0 1
total: 1 1
0: 1 .
1: . .
2: . .
3: . .
4: . .
5: . .
6: . .
7: . .
8: . .
9: . .
10: . .
11: . .
12: . .
13: . .
14: . .
15: . .
16: . .
17: . .
18: . .
19: . 1
-- hollow triangles of lengths 2, 3, and 4
for k from 2 to 4 do (
A = homogenizeLatticePoints hollowPolygon transpose matrix {{0,0}, {k,0}, {0,k}};
print minimalBetti latticeIdeal A;
print "\n"
)
0 1 2 3
total: 1 6 8 3
0: 1 . . .
1: . 6 8 3
0 1 2 3 4 5 6 7 8
total: 1 17 53 91 108 83 37 9 1
0: 1 . . . . . . . .
1: . 17 43 36 8 . . . .
2: . . 10 55 100 83 37 9 1
0 1 2 3 4 5 6 7 8 9 10 11
total: 1 33 153 525 1356 2178 2205 1486 675 201 36 3
0: 1 . . . . . . . . . . .
1: . 33 123 144 30 . . . . . . .
2: . . 30 381 1326 2178 2205 1486 675 201 36 3
-- hollow squares of lengths 2, 3
for k from 2 to 3 do (
A = homogenizeLatticePoints hollowPolygon transpose matrix {{0,0}, {k,0}, {0,k}, {k,k}};
print minimalBetti latticeIdeal A;
print "\n"
)
0 1 2 3 4 5 6 7
total: 1 11 34 57 55 29 8 1
0: 1 . . . . . . .
1: . 11 17 6 . . . .
2: . . 17 51 55 29 8 1
0 1 2 3 4 5 6 7 8 9 10 11
total: 1 29 232 942 2176 3154 3045 2008 903 268 48 4
0: 1 . . . . . . . . . . .
1: . 29 84 90 48 10 . . . . . .
2: . . 148 852 2128 3144 3045 2008 903 268 48 4
Theorem: $\text{reg}(\triangle^k) = 2$ for all $k \geq 3$.
Theorem: $\text{reg}(\square^k) = 2$ for all $k \geq 2$.
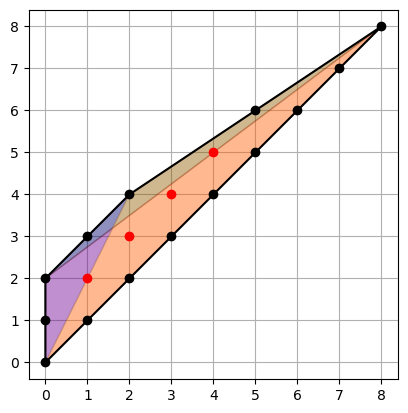
Proofs involve representing interior points as $\mathbb{N}$-linear combinations of the boundary points. Taking "enough" points on the boundary should decrease the regularity.
-- Example: smooth is not enough
A = hollowPolygon homogenizeLatticePoints transpose matrix {{0,0}, {0,2}, {2,4}, {8,8}}
print minimalBetti latticeIdeal A; -- regularity = 3
0 1 2 3 4 5 6 7 8 9 10 11 12 13
total: 1 54 385 1462 3608 6456 8394 7875 5369 2639 913 212 30 2
0: 1 . . . . . . . . . . . . .
1: . 52 280 730 1128 1050 720 315 80 9 . . . .
2: . . 81 600 2040 4416 6090 5712 3705 1640 473 80 6 .
3: . 2 24 132 440 990 1584 1848 1584 990 440 132 24 2