Doing research mathematics does not consist solely of ruminating alone in a darkened room, but also of rolling up ones sleeves, writing some code, and having the computer do the legwork.
Lefschetz properties¶
Artinian algebras¶
Definition: A $\mathbb{Z}$-graded $\mathbb{K}$-algebra $A$ is Artinian if $A_d = 0$ for $d \gg 0$.
Example: $A = \mathbb{K}[x,y,z] / \langle x^2,y^2,z^3 \rangle$
| $d$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | |
|---|---|---|---|---|---|---|---|
| $\text{gens}(A_d)$ | $1$ | $x$ $y$ $z$ |
$xy$ $xz$ $yz$ $z^2$ |
$xyz$ $xz^2$ $yz^2$ |
$xyz^2$ | $\emptyset$ | |
| $\text{dim}(A_d)$ | $1$ | $3$ | $4$ | $3$ | $1$ | $0$ |
Example: If $I_\Delta \subseteq \mathbb{K}[x_1,\dots,x_n]$ is a Stanley-Reisner ideal, then $I_\Delta + \langle x_i^2 \, | \, 1 \leq i \leq n \rangle$ is Artinian.
kk = ZZ/32749
R = kk[x,y,z]
I = ideal(x^2, y^2, z^3)
A = R/I
-- why do by hand what you can do by computer...?
ds = {"d"} | for i in 0..5 list i
mons = {"gens(A_d)"} | for i in 0..5 list netList(flatten entries basis(i, A), Boxes=>false)
dims = {"dim(A_d)"} | for i in 0..5 list hilbertFunction(i, A)
print netList({ds} | {mons} | {dims}, HorizontalSpace=>2, VerticalSpace=>1, Alignment=>Center)
+-------------+-----+-----+-------+---------+----------+-----+ | | | | | | | | | d | 0 | 1 | 2 | 3 | 4 | 5 | | | | | | | | | +-------------+-----+-----+-------+---------+----------+-----+ | | | | | | | | | | | | | | 2 | | | gens(A_d) | 1 | x | x*y | x*y*z | x*y*z | | | | | y | x*z | 2 | | | | | | z | y*z | x*z | | | | | | | 2 | 2 | | | | | | | z | y*z | | | | | | | | | | | +-------------+-----+-----+-------+---------+----------+-----+ | | | | | | | | | dim(A_d) | 1 | 3 | 4 | 3 | 1 | 0 | | | | | | | | | +-------------+-----+-----+-------+---------+----------+-----+
-- Artinian => Hilbert series is a polynomial
print("Hilbert series: " | toString(hilbertSeries(A, Reduce=>true)))
Hilbert series: (1+3*T+4*T^2+3*T^3+T^4)/(1)
-- Artinian <=> Krull dim = 0
print("R/I = " | toString(describe(A)) |
" is Artinian: " | toString(dim(A) == 0))
R/I = R/(x^2,y^2,z^3) is Artinian: true
Weak Lefschetz property (WLP)¶
For all $f \in A$, $f$ is a zero-divisor. The best we can hope for is $\exists \, f \in A$ such that $\cdot f$ is injective or surjective in all degrees.
Definition: $A = R/I$ has the weak Lefschetz property (WLP) if $A_i \xrightarrow{\cdot \ell} A_{i+1}$ is full rank (i.e., either injective or surjective) for all $i \geq 0$. If $A_i \xrightarrow{\cdot \ell^d} A_{i+d}$ is full rank for all $i$ and $d$, then we say $A$ has the strong Lefschetz property (SLP).
Who cares?¶
Commutative algebra
- Fröberg's conjecture
- Growth of Hilbert functions
Conjecture [Froberg; 1985]: Let $f_1, \dots, f_s \subset R = \mathbb{K}[x_1, \dots, x_r]$ be generic forms with degrees $d_1, \dots, d_s$, respectively, and let $I = \langle f_1, \dots, f_s \rangle$. Then $$ \text{HS}_{S/I}(t) = \left[ \frac{\prod_{i=1}^s (1 - t^{d_i})}{(1 - t)^n} \right],$$ where the series is truncated at its first negative term.
Who cares?¶
Geometric combinatorics
- $g$-theorem (formerly McMullen's conjecture)
- log-concavity of sequences (e.g., $f$-vectors)
- top-heavy theorem (easy* way of getting a Field's medal)
WLP is hard¶
Theorem [Brenner, Kaid; 2010]
Let $\text{char}(\mathbb{K}) = 2$. Then $A = \mathbb{K}[x,y,z] / \langle x^d, y^d, z^d \rangle$ has the WLP if and only if $d = \left\lfloor \frac{2^k + 1}{3} \right\rfloor$ for some positive integer $k$.
Theorem [Harbourne, Schenck, Seceleanu; 2011]
Let $$ I = \langle L_1^t, \dots, L_n^t \rangle \subset \mathbb{K}[x_1,x_2,x_3,x_4] $$ with $L_i \in R_1$ generic. If $n \in \{5,6,7,8\}$, then the WLP fails, respectively, for $t \geq \{3,27,140,704\}$.
Question
Does every complete intersection in four or more variables have the WLP?
Start with geometry¶
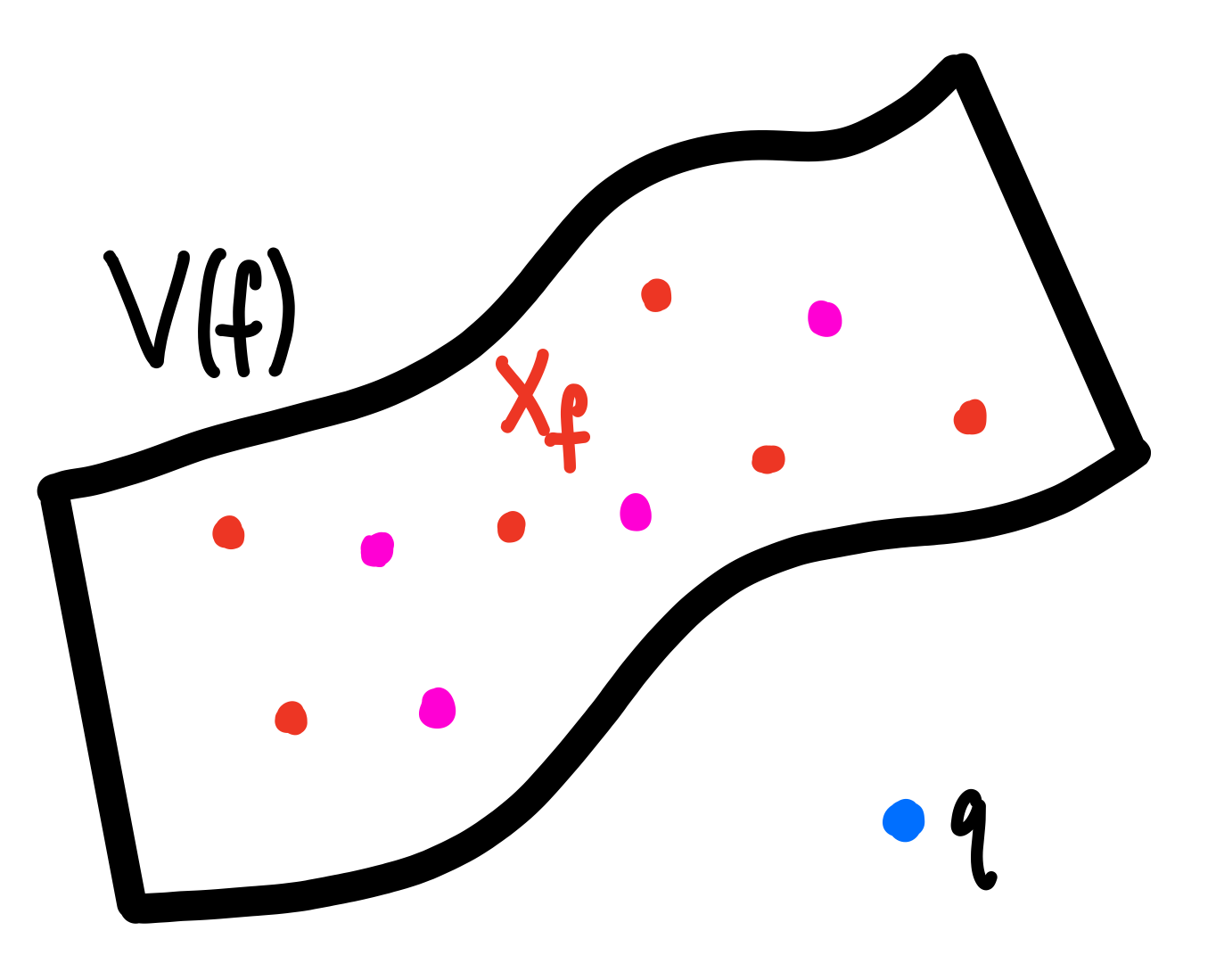
Theorem [G., Schenck]: Let $X_f \subset \mathbb{P}^n$ be a set of distinct points lying on a distinct points lying on a unique hypersurface $\mathbf{V}(f)$ with $\text{deg}(f) = d$ such that $\mathbf{I}(X_f) = (f)$. Choose $q \not\in \mathbf{V}(f)$ such that if $X = X_f \cup \{f\}$, then $$\mathbf{I}(X)_d = 0 \quad \text{and} \quad \text{dim}_{\mathbb{K}}(\mathbf{I}(X)_{d+1}) = n.$$ Then the Artinian reduction $A_X$ does not have the WLP. In particular, if $I$ is a general linear form, then $A_d \xrightarrow{\cdot l} A_{d+1}$ does not have full rank.
Betti tables¶
Given an ideal $I \subset \mathbb{K}[x_1,\dots,x_n]$, a (minimal) free resolution "approximates" $R/I$. The betti table records the ranks of the summands appearing in the free resolution.
Example: $R = \mathbb{K}[x,y,z]$ and $I = \langle x^2, y^2, z^3 \rangle$ $$0 \leftarrow R/I \leftarrow R \leftarrow \substack{R(-2)^2 \\ \oplus \\ R(-3)} \leftarrow \substack{R(-4) \\ \oplus \\ R(-5)^2} \leftarrow R(-7) \leftarrow 0$$
F = res I
-- resolution and summands
print F
1 3 3 1
R <-- R <-- R <-- R <-- 0
0 1 2 3 4
-- differentials in the complex
print F.dd
1 3
0 : R <---------------- R : 1
| x2 y2 z3 |
3 3
1 : R <----------------------- R : 2
{2} | -y2 -z3 0 |
{2} | x2 0 -z3 |
{3} | 0 x2 y2 |
3 1
2 : R <--------------- R : 3
{4} | z3 |
{5} | -y2 |
{5} | x2 |
1
3 : R <----- 0 : 4
0
-- summands in free resolution
for i in 0..length(F) do print(toString(i) | ": " | toString flatten degrees F_i)
-- Betti table
print betti F
-- invariants from Betti table
print("Projective dimension of R/I: " | toString pdim (R^1/I))
print("Regularity of R/I: " | toString regularity(R^1/I))
0: {0}
1: {2, 2, 3}
2: {4, 5, 5}
3: {7}
0 1 2 3
total: 1 3 3 1
0: 1 . . .
1: . 2 . .
2: . 1 1 .
3: . . 2 .
4: . . . 1
Projective dimension of R/I: 3
Regularity of R/I: 4
Koszul tails¶
Definition: A Betti table $B$ has an $(n,d)$-Koszul tail if it has an upper-left principal block of the form $$ \begin{array}{c|ccccccccc} & 0 & 1 & 2 & 3 & \dots & n-2 & n-1 & n & n+1 \\ \hline 0 & 1 & . & . & . & \dots & . & . & . & * \\ 1 & . & . & . & . & \dots & . & . & . & * \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & * \\ d-1 & . & . & . & . & \dots & . & . & . & * \\ d & . & n & \binom{n}{2} & \binom{n}{3} & \dots & \binom{n}{n-2} & n & 1 & * \\ d+1 & * & * & * & * & * & * & * & * & * \end{array}. $$ If $B$ is has an $(n,d)$-Koszul tail and is the Betti table for an Artinian ring $\mathbb{K}[x_1,\dots,x_n]/I$, then we say $B$ has a maximal $(n,d)$-Koszul tail.
kk = ZZ/32749
R = kk[x_1..x_4]
allPoints = transpose matrix{{1,0,0,0},{0,1,0,0},{1,1,1,0},{0,0,1,0},{0,1,1,0},{1,1,0,0},{1,0,1,0},{0,0,0,1}}**kk
-- compute the Artinian reduction
Ired = Ared sub(pointsIdeal allPoints, R)
print allPoints
print minimalBetti ideal Ired
print("Has WLP: " | toString(checkWLP ideal Ired))
| 1 0 1 0 0 1 1 0 |
| 0 1 1 0 1 1 0 0 |
| 0 0 1 1 1 0 1 0 |
| 0 0 0 0 0 0 0 1 |
0 1 2 3
total: 1 6 8 3
0: 1 . . .
1: . 3 3 1
2: . 3 4 1
3: . . 1 1
Has WLP: false
Results¶
Theorem [G., Schenck; 2023]
An Artinian algebra $A = \mathbb{K}[x_1,\dots,x_n]/I$ whose Betti table has a maximal $(n,d)$-Koszul tail does not have the WLP.
Corollary
If $T = \mathbb{K}[x_1,\dots,x_n]/I$ is Cohen-Macaulay of dimension $m$, and the Betti table of $T$ has a maximal $(n-m,d)$-Koszul tail, then the Artinian reduction of $T$ does not have the WLP.
Corollary
If $A = \mathbb{K}[x_1,\dots,x_{m+n}]/I$ is Artinian with an $(n,d)$-Koszul tail, and there exists a sequence of linearly independent linear forms $\{l_1,\dots,l_m\}$ such that the Betti tables of $A$ and $A/I_L$ have the same top row, then $A/I_L$ does not have the WLP.
-- Koszul tail is not sufficient
kk = ZZ/32749
R = kk[x_1..x_4]
I = ideal(x_4^2, x_3*x_4, x_3^3, x_2 * x_3^2 - x_2^2 * x_4, x_1 * x_3^2 - x_1 * x_2 * x_4 + x_2^2 * x_4, x_2^2 * x_3, x_2^3, x_1^3 * x_4 - x_1^2 * x_2 * x_4 + x_1 * x_2^2 * x_4, x_1^3 * x_3, x_1^3 * x_2 - x_1^2 * x_2^2, x_1^4)
J = ideal(x_1 * x_4, x_1^2, x_3 * x_4^2, x_2 * x_4^2, x_2^2 * x_4, x_1 * x_3^2, x_1 * x_2^2 - x_3^2 * x_4, x_3^4, x_2 * x_3^3 - x_4^4, x_2^2 * x_3^2, x_2^4)
print netList({{"Betti(I)", "Betti(J)"}, {minimalBetti I, minimalBetti J}}, HorizontalSpace=>2, VerticalSpace=>1, Alignment=>Center)
+-----------------------+-----------------------+ | | | | Betti(I) | Betti(J) | | | | +-----------------------+-----------------------+ | | | | 0 1 2 3 4 | 0 1 2 3 4 | | total: 1 11 20 11 1 | total: 1 11 20 11 1 | | 0: 1 . . . . | 0: 1 . . . . | | 1: . 2 1 . . | 1: . 2 1 . . | | 2: . 5 9 4 . | 2: . 5 9 4 . | | 3: . 4 9 5 . | 3: . 4 9 5 . | | 4: . . 1 2 . | 4: . . 1 2 . | | 5: . . . . 1 | 5: . . . . 1 | | | | +-----------------------+-----------------------+
Future work¶
- Can we do better than a Koszul tail? Having a Koszul tail is very strict.
- Is there a "nice" Boij-Söderberg theory underlying this?
- Characterize the Stanley-Reisner rings whose Artinian reductions have a Koszul tail.