Doing research mathematics does not consist solely of ruminating alone in a darkened room, but also of rolling up ones sleeves, writing some code, and having the computer do the legwork.
Overview¶
- Lefschetz properties
- Hypersurfaces
- Betti tables
- Toric varieties
- Castelnuovo-Mumford regularity
- Lattice points and toric surfaces
- Other projects
MatrixSchubertpackage for Macaulay2 (published in JSAG)- Betti numbers of connected sums (published in TAMS)
- Graph Theoretic Reflection to Foster Alignment in Coordinated Course (resubmitted)
Lefschetz properties¶
Artinian algebras¶
Definition: A $\mathbb{Z}$-graded $\mathbb{K}$-algebra $A$ is Artinian if $A_d = 0$ for $d \gg 0$.
Example: $A = \mathbb{K}[x,y,z] / \langle x^2,y^2,z^3 \rangle$
| $d$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | |
|---|---|---|---|---|---|---|---|
| $\text{gens}(A_d)$ | $1$ | $x$ $y$ $z$ |
$xy$ $xz$ $yz$ $z^2$ |
$xyz$ $xz^2$ $yz^2$ |
$xyz^2$ | $\emptyset$ | |
| $\text{dim}(A_d)$ | $1$ | $3$ | $4$ | $3$ | $1$ | $0$ |
Example: If $I_\Delta \subseteq \mathbb{K}[x_1,\dots,x_n]$ is a Stanley-Reisner ideal, then $I_\Delta + \langle x_i^2 \, | \, 1 \leq i \leq n \rangle$ is Artinian.
Weak Lefschetz property (WLP)¶
For all $f \in A$, $f$ is a zero-divisor. The best we can hope for is $\exists \, f \in A$ such that $\cdot f$ is injective or surjective in all degrees.
Definition: $A = R/I$ has the weak Lefschetz property (WLP) if $A_i \xrightarrow{\cdot \ell} A_{i+1}$ is full rank (i.e., either injective or surjective) for all $i \geq 0$.
Who cares?¶
Proposition: Suppose $A$ is a standard graded Artinian $\mathbb{K}$-algebra. If $A$ has the WLP, then $A$ has a unimodal Hilbert function.
Geometric combinatorics¶
- $g$-theorem (formerly McMullen's conjecture)
- log-concavity of sequences (e.g., $f$-vectors)
- top-heavy theorem
Commutative algebra¶
- Conjecture [Fröberg, 1985]: Suppose $f_1,\dots,f_r \in R = \mathbb{K}[x_1,\dots,x_n]$ are generic forms of degrees $d_1,\dots,d_r$, respectively, and let $I = \langle f_1,\dots,f_r \rangle$. Then $$\text{HS}_{R/I}(t) = \left[ \frac{\prod_{k=1}^r (1 - t^{d_k})}{(1-t)^n} \right],$$
where $[ \dots ]$ denotes truncation at the first negative terms of the series.
- Growth of Hilbert functions
WLP is hard¶
Theorem [Brenner-Kaid, 2010]: Let $\text{char}(\mathbb{K}) = 2$. Then $A = \mathbb{K}[x,y,z] / \langle x^d, y^d, z^d \rangle$ has the WLP if and only if $d = \left\lfloor \frac{2^k + 1}{3} \right\rfloor$ for some positive integer $k$.
Theorem [Harbourne-Schenck-Seceleanu, 2011]: Let $$ I = \langle L_1^t, \dots, L_n^t \rangle \subset \mathbb{K}[x_1,x_2,x_3,x_4] $$ with $L_i \in R_1$ generic. If $n \in \{5,6,7,8\}$, then the WLP fails, respectively, for $t \geq \{3,27,140,704\}$.
Question: Does every complete intersection in four or more variables have the WLP?
Start with geometry¶
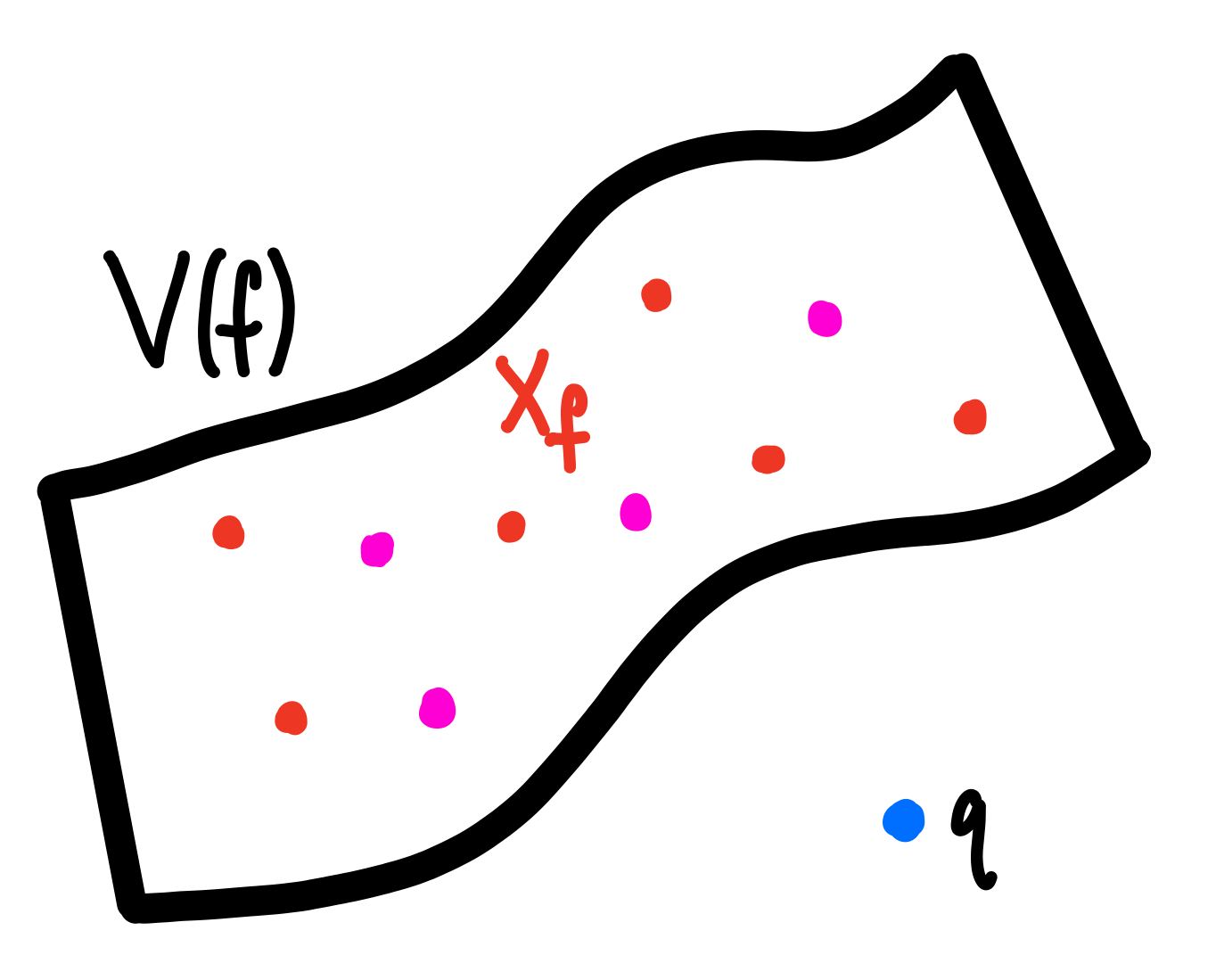
Theorem [G.-Schenck, 2024]: Let $X_f \subset \mathbb{P}^n$ be a set of distinct points lying on a distinct points lying on a unique hypersurface $\mathbf{V}(f)$ with $\text{deg}(f) = d$ such that $\mathbf{I}(X_f) = (f)$. Choose $q \not\in \mathbf{V}(f)$ such that if $X = X_f \cup \{f\}$, then $$\mathbf{I}(X)_d = 0 \quad \text{and} \quad \text{dim}_{\mathbb{K}}(\mathbf{I}(X)_{d+1}) = n.$$ Then the Artinian reduction $A_X$ does not have the WLP. In particular, if $I$ is a general linear form, then $A_d \xrightarrow{\cdot \ell} A_{d+1}$ does not have full rank.
Betti tables¶
Given an ideal $I \subset \mathbb{K}[x_1,\dots,x_n]$, a (minimal) free resolution "approximates" $R/I$. The Betti table records the ranks of the summands appearing in the free resolution.
Example: $R = \mathbb{K}[x,y,z]$ and $I = \langle x^2, y^2, z^3 \rangle$ $$0 \leftarrow R/I \leftarrow R \leftarrow \substack{R(-2)^2 \\ \oplus \\ R(-3)} \leftarrow \substack{R(-4) \\ \oplus \\ R(-5)^2} \leftarrow R(-7) \leftarrow 0$$
$$0 \leftarrow R/I \leftarrow R \leftarrow \substack{R(-(1+1))^2 \\ \oplus \\ R(-(1+2))} \leftarrow \substack{R(-(2+2)) \\ \oplus \\ R(-(2+3))^2} \leftarrow R(-(3+4)) \leftarrow 0$$
-- summands in free resolution
for i in 0..length(F) do print(toString(i) | ": " | toString flatten degrees F_i)
-- Betti table
print betti F
-- invariants from Betti table
print("Projective dimension of R/I: " | toString pdim (R^1/I))
print("Regularity of R/I: " | toString regularity(R^1/I))
0: {0}
1: {2, 2, 3}
2: {4, 5, 5}
3: {7}
0 1 2 3
total: 1 3 3 1
0: 1 . . .
1: . 2 . .
2: . 1 1 .
3: . . 2 .
4: . . . 1
Projective dimension of R/I: 3
Regularity of R/I: 4
Koszul tails¶
Definition: A Betti table $B$ has an $(n,d)$-Koszul tail if it has an upper-left principal block of the form $$ \begin{array}{c|ccccccccc} & 0 & 1 & 2 & 3 & \dots & n-2 & n-1 & n & n+1 \\ \hline 0 & 1 & . & . & . & \dots & . & . & . & * \\ 1 & . & . & . & . & \dots & . & . & . & * \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & * \\ d-1 & . & . & . & . & \dots & . & . & . & * \\ d & . & n & \binom{n}{2} & \binom{n}{3} & \dots & \binom{n}{n-2} & n & 1 & * \\ d+1 & * & * & * & * & * & * & * & * & * \end{array}. $$ If $B$ is has an $(n,d)$-Koszul tail and is the Betti table for an Artinian ring $\mathbb{K}[x_1,\dots,x_n]/I$, then we say $B$ has a maximal $(n,d)$-Koszul tail.
Koszul tails¶
kk = ZZ/32749
R = kk[x_1..x_4]
allPoints = transpose matrix{{1,0,0,0},{0,1,0,0},{1,1,1,0},{0,0,1,0},{0,1,1,0},{1,1,0,0},{1,0,1,0},{0,0,0,1}}**kk
-- compute the Artinian reduction
Ired = Ared sub(pointsIdeal allPoints, R)
print allPoints
print minimalBetti ideal Ired
print("Has WLP: " | toString(checkWLP ideal Ired))
| 1 0 1 0 0 1 1 0 |
| 0 1 1 0 1 1 0 0 |
| 0 0 1 1 1 0 1 0 |
| 0 0 0 0 0 0 0 1 |
0 1 2 3
total: 1 6 8 3
0: 1 . . .
1: . 3 3 1
2: . 3 4 1
3: . . 1 1
Has WLP: false
Results¶
Theorem [G.-Schenck, 2024]: An Artinian algebra $A = \mathbb{K}[x_1,\dots,x_n]/I$ whose Betti table has a maximal $(n,d)$-Koszul tail does not have the WLP.
Corollary: If $T = \mathbb{K}[x_1,\dots,x_n]/I$ is Cohen-Macaulay of dimension $m$, and the Betti table of $T$ has a maximal $(n-m,d)$-Koszul tail, then the Artinian reduction of $T$ does not have the WLP.
Corollary: If $A = \mathbb{K}[x_1,\dots,x_{m+n}]/I$ is Artinian with an $(n,d)$-Koszul tail, and there exists a sequence of linearly independent linear forms $\{l_1,\dots,l_m\}$ such that the Betti tables of $A$ and $A/I_L$ have the same top row, then $A/I_L$ does not have the WLP.
Future work¶
- Can we do better than a Koszul tail? Having a Koszul tail is very strict.
- Is there a "nice" Boij-Söderberg theory underlying this?
- Characterize the Stanley-Reisner rings whose Artinian reductions have a Koszul tail.
Toric Varieties¶
Lattice points¶
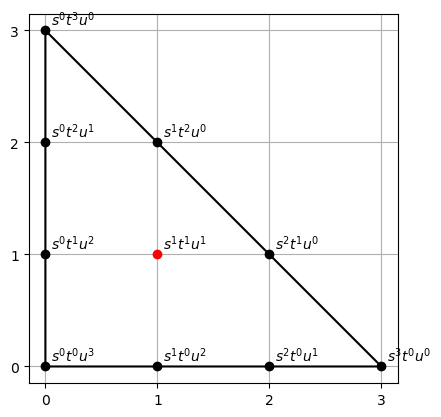
A set of lattice points, represented as the columns of the $d \times n$ matrix defines a monomial map.
Example
$$ A = \begin{pmatrix} d & d-1 & \dots & 1 & 0 \\ 0 & 1 & \dots & d-1 & d \end{pmatrix} $$$A$ consists of the integral points on the line $x+y=d$ with $x,y \geq 0$. It defines the monomial curve $C$ given as the image of the map
$$(s,t) \longmapsto (s^d, s^{d-1} t, \dots, s t^{d-1}, t^d).$$The kernel of this map defines the toric ideal $I_C$.
Example: twisted cubic¶
$$A = \begin{pmatrix} 3 & 2 & 1 & 0 \\ 0 & 1 & 2 & 3 \end{pmatrix}$$The monomial curve $C$ is the image of the map $(s,t) \mapsto (s^3, s^2 t, s t^2, t^3)$. Set $$x_0 = s^3, \quad x_1 = s^2 t, \quad x_2 = s t^2, \quad x_3 = t^3.$$ Then $$I_C = \langle x_1 x_2 - x_0 x_3, x_1^2 - x_0 x_2, x_2^2 - x_1 x_3 \rangle.$$
-- twisted cubic
kk = ZZ/32749
R = kk[x_0..x_3]
I = monomialCurveIdeal(R, {1,2,3})
print I
print betti res I
2 2
ideal (x - x x , x x - x x , x - x x )
2 1 3 1 2 0 3 1 0 2
0 1 2
total: 1 3 2
0: 1 . .
1: . 3 2
Castelnuovo-Mumford regularity¶
Definition: Let $I \subseteq R = \mathbb{K}[x_0,\dots,x_n]$ be a homogeneous ideal, and consider the minimal free resolution $$0 \leftarrow R/I \leftarrow F_0 \leftarrow \dots \leftarrow F_{n+1} \leftarrow 0$$ of $R/I$, where $F_i \cong \bigoplus_j R(-i-j)^{\beta_{i,j}}$. The Castelnuovo-Mumford regularity (or simply regularity) is $$\text{reg}(R/I) = \max_{i,j} \left\{ j \, \colon \, \beta_{i,j} \neq 0 \right\}.$$
Note: The regularity is the index of the bottom row in the Betti table.
Castelnuovo-Mumford regularity¶
Definition: A coherent sheaf on $\mathbb{P}^n$ is $m$-regular if $$H^i(\mathscr{F}(m-i)) = 0$$ for all $i > 0$. The regularity is $$\inf \{d \, \colon \, H^i(\mathscr{F}(d-i)) = 0 \, \text{ for all } i > 0 \}.$$
Regularity of monomial curves¶
Theorem [L'vovsky, 1996]: Let $A = (0,a_1,\dots,a_n)$ be a sequence of non-negative integers such that the g.c.d. of the $a_j$'s equals $1$, and let $C$ be the corresponding monomial curve. Then $C$ is $m$-regular, where $$m = \max_{1 \leq i < j \leq n} \{ (a_i - a_{i-1}) + (a_j - a_{j-1}) \},$$ i.e., $m$ is the sum of the two largest gaps in the semigroup generated by $A$.
-- twisted cubic
I = monomialCurveIdeal(kk[x_0..x_3], {1,2,3})
print betti res I
print(toString I | " -> reg(I) = " | toString regularity I)
-- sporadic
I = monomialCurveIdeal(kk[x_0..x_4], {1,3,5,8})
print betti res I
print(toString I | " -> reg(I) = " | toString regularity I)
0 1 2
total: 1 3 2
0: 1 . .
1: . 3 2
ideal(x_2^2-x_1*x_3,x_1*x_2-x_0*x_3,x_1^2-x_0*x_2) -> reg(I) = 2
0 1 2 3 4
total: 1 6 9 5 1
0: 1 . . . .
1: . 2 . . .
2: . 3 6 1 .
3: . 1 3 4 1
ideal(x_2*x_3-x_0*x_4,x_2^2-x_1*x_3,x_1*x_3^2-x_0*x_2*x_4,x_0*x_3^2-x_1^2*x_4,x_1^2*x_2-x_0^2*x_3,x_1^3-x_0^2*x_2,x_3^4-x_1*x_2*x_4^2) -> reg(I) = 4
Example: sporadic monomial curve¶

Consider the curve parameterized by $(0,3,5,7)$. The monomial map paramaterizing the monomial curve $C$ is given by $$\varphi(s,t) = (\underset{\color{red} x_0}{s^7}, \quad \underset{\color{red} x_1}{s^3 t^4}, \quad \underset{\color{red} x_2}{s^5 t^2}, \quad \underset{\color{red} x_3}{t^7})$$ with defining ideal $$I_C = \langle x_2^2 - x_1 x_3, \quad x_1^3 x_2 - x_0^2 x_3^2, \quad x_1^4 - x_0^2 x_2 x_3 \rangle \subseteq R = \mathbb{K}[x_0,x_1,x_2,x_3].$$
The coordinate ring has the following minimal free resolution: $$0 \leftarrow R/I_C \leftarrow R \leftarrow \substack{R(-2)\\\oplus\\R(-4)^2} \leftarrow R(-5)^2 \leftarrow 0.$$ Using L'vovsky's result, we get a bound on the regularity without the need to compute a minimal free resolution. $$\text{reg}(I_C) = 4 \leq (a_1 - a_0) + (a_2 - a_1) = 3 + 2 = 5.$$
Regularity of toric surfaces¶
Now working with lattice points in the plane (and then homogenizing).
Examples
-- Veronese
A = homogenizeLatticePoints transpose matrix {{0,0},{1,0},{2,0},{3,0},{0,1},{1,1},{2,1},{0,2},{1,2},{0,3}}
I = latticeIdeal A
print A
print minimalBetti I
| 0 1 2 3 0 1 2 0 1 0 |
| 0 0 0 0 1 1 1 2 2 3 |
| 3 2 1 0 2 1 0 1 0 0 |
0 1 2 3 4 5 6 7
total: 1 27 105 189 189 105 27 1
0: 1 . . . . . . .
1: . 27 105 189 189 105 27 .
2: . . . . . . . 1
-- badBoy example from Hal
A = transpose matrix{{0,0},{7,3},{4,4},{2,3}}
I = latticeIdeal homogenizeLatticePoints A
print I
print betti res I -- regularity = 19
5 15 4 16
ideal(x x - x x )
0 2 1 3
0 1
total: 1 1
0: 1 .
1: . .
2: . .
3: . .
4: . .
5: . .
6: . .
7: . .
8: . .
9: . .
10: . .
11: . .
12: . .
13: . .
14: . .
15: . .
16: . .
17: . .
18: . .
19: . 1
Past work¶
- Conjecture [Eisenbud-Goto, 1984]: Let $\mathbb{K}$ be algebraically closed, and let $I \subseteq R = \mathbb{K}[x_1,\dots,x_n]$ be a nondegenerate prime ideal. Then $$\text{reg}(R/I) \leq \deg(I) - \text{codim}(I).$$
- Theorem [Gruson-Lazarsfeld-Peskine, 1983]: Let $C \subseteq \mathbb{P}^n$ be a reduced nondegenerate curve. Then $$\text{reg}(I_C) \leq \deg(C) - n + 2.$$
- Theorem [Lazarsfeld, 1997]: Every smooth, projective surface satisfies the Eisenbud-Goto conjecture.
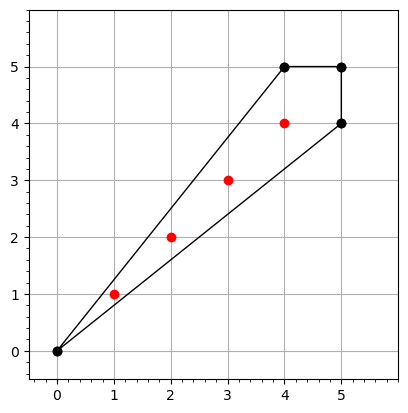
- Theorem [Koelman, 1993]: For a lattice polygon $P$, the ideal $I_P$ is generated by quadric and cubic binomials. Moreover, all of the minimal generators of $I_P$ are quadrics if and only if $|\partial P| > 3$.
- Theorem [Schenck, 2004; Hering, 2006]: If $P$ has nonempty interior, then the index where $\beta_{i,i+2}$ is first nonzero is $|\partial P|$.
Hollow regular polygons¶
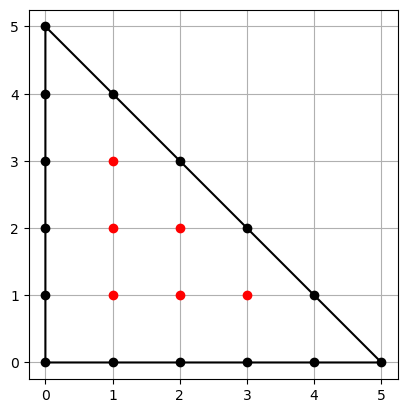
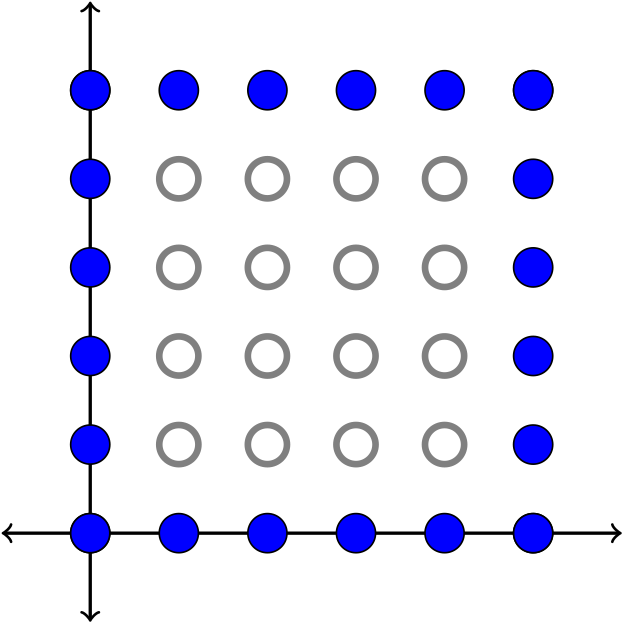
Setup¶
$$ \begin{array}{c} A = \begin{pmatrix} 0 & 0 & 3 \\ 0 & 3 & 0 \end{pmatrix} \\ \, \\ \hspace{2cm} \downarrow \hspace{0.5cm} \text{Conv}(A) \setminus \text{Int}(A) \\ \, \\ \begin{pmatrix} 0 & 1 & 2 & \cdots & 0 & 0 & 0 \\ 0 & 0 & 0 & \cdots & 3 & 2 & 1 \end{pmatrix} \\ \, \\ \hspace{1cm} \downarrow \hspace{0.5cm} \text{homogenize} \\ \, \\ \tilde{A} = \begin{pmatrix} 0 & 1 & 2 & \cdots & 0 & 0 & 0 \\ 0 & 0 & 0 & \cdots & 3 & 2 & 1 \\ 3 & 2 & 1 & \cdots & 0 & 1 & 2 \end{pmatrix} \end{array} $$
''Bad boy''¶
In general, the regularity can be arbitrarily large by using $$A = \begin{pmatrix} 0 & d & d-1 & d \\ 0 & d-1 & d & d \end{pmatrix}.$$

Hollow triangles¶
Definition: Suppose $A = \begin{pmatrix} 0 & k & 0 \\ 0 & 0 & k \end{pmatrix}$. The hollow triangle of length $k$ is $\triangle^k = \tilde{A}$.
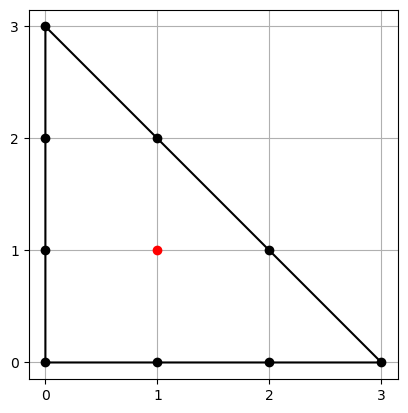

-- hollow triangles of lengths 2, 3, and 4
for k from 2 to 4 do (
A = hollowPolygon homogenizeLatticePoints transpose matrix{{0,0},{k,0},{0,k}};
print minimalBetti(latticeIdeal A);
print "\n"
)
0 1 2 3
total: 1 6 8 3
0: 1 . . .
1: . 6 8 3
0 1 2 3 4 5 6 7 8
total: 1 17 53 91 108 83 37 9 1
0: 1 . . . . . . . .
1: . 17 43 36 8 . . . .
2: . . 10 55 100 83 37 9 1
0 1 2 3 4 5 6 7 8 9 10 11
total: 1 33 153 525 1356 2178 2205 1486 675 201 36 3
0: 1 . . . . . . . . . . .
1: . 33 123 144 30 . . . . . . .
2: . . 30 381 1326 2178 2205 1486 675 201 36 3
Hollow squares¶
Definition: Suppose $A = \begin{pmatrix} 0 & k & 0 & k \\ 0 & 0 & k & k \end{pmatrix}$. The hollow square of length $k$ is $\square^k = \tilde{A}$.

-- hollow squares of lengths 2, 3
for k from 2 to 4 do (
A = hollowPolygon homogenizeLatticePoints transpose matrix{{0,0},{k,0},{0,k},{k,k}};
print minimalBetti(latticeIdeal A);
print "\n"
)
0 1 2 3 4 5 6 7
total: 1 11 34 57 55 29 8 1
0: 1 . . . . . . .
1: . 11 17 6 . . . .
2: . . 17 51 55 29 8 1
0 1 2 3 4 5 6 7 8 9 10 11
total: 1 29 232 942 2176 3154 3045 2008 903 268 48 4
0: 1 . . . . . . . . . . .
1: . 29 84 90 48 10 . . . . . .
2: . . 148 852 2128 3144 3045 2008 903 268 48 4
o28 = [KERNEL ENFORCED TIMEOUT]
Hollow triangles/squares have low regularity¶
Theorem: $\text{reg}(\triangle^k) = 2$ for all $k \geq 3$.
Theorem: $\text{reg}(\square^k) = 2$ for all $k \geq 3$.
Key lemma¶
Lemma: For all $d \geq 2$, $(R/I_{\square^k})_d = (\overline{R/I_{\square^k}})_d$.
Proof sketch of theorem
- Use the short exact sequence of sheaves $$0 \to \mathscr{I}_{\square^k}(d) \to \mathscr{O}_{\mathbb{P}^{4k-1}}(d) \to \mathscr{O}_{\square^k}(d) \to 0$$ to eventually get a short exact sequence $$0 \to R/I_{\square^k} \to \overline{R/I_{\square^k}} \to N \to 0$$.
- By the lemma, $N$ is only generated by degree $1$ monomials.
- $\text{reg}(R/I_{\square^k}) \leq \max(\text{reg}(\overline{R/I_{\square^k}}), N) = \text{reg}(\overline{R/I_{\square^k}}) = 2$.
Proof of lemma for $\square^k$¶
- Showing $(R/I_{\square^k})_d = (\overline{R/I_{\square^k}})_d$ for $d \geq 2$ amounts to a computation with the lattice points of $\square^k$.
- We are done if for any $p_1,p_2 \in \overline{\square^k}$, we can write $p_1 + p_2 = q_1 + q_2$ with $q_1,q_2 \in \square^k$.
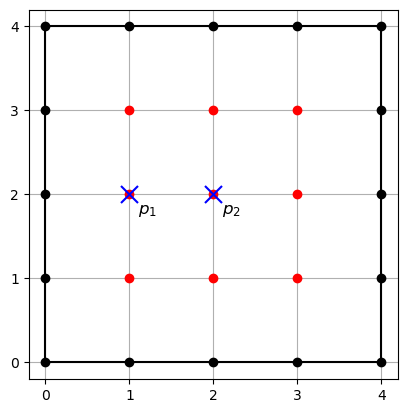
$$ \begin{align*} p_1 + p_2 &= \begin{pmatrix} 1 \\ 2 \\ 5 \end{pmatrix} + \begin{pmatrix} 2 \\ 2 \\ 4 \end{pmatrix} = \begin{pmatrix} 3 \\ 4 \\ 9 \end{pmatrix} \\ &\phantom{= \begin{pmatrix} 0 \\ 2 \\ 6 \end{pmatrix} + \begin{pmatrix} 3 \\ 2 \\ 3 \end{pmatrix}} \\ &\phantom{= \begin{pmatrix} 0 \\ 0 \\ 8 \end{pmatrix} + \begin{pmatrix} 3 \\ 4 \\ 1 \end{pmatrix}} \end{align*} $$
Proof of lemma for $\square^k$¶
- Showing $(R/I_{\square^k})_d = (\overline{R/I_{\square^k}})_d$ for $d \geq 2$ amounts to a computation with the lattice points of $\square^k$.
- We are done if for any $p_1,p_2 \in \overline{\square^k}$, we can write $p_1 + p_2 = q_1 + q_2$ with $q_1,q_2 \in \square^k$.
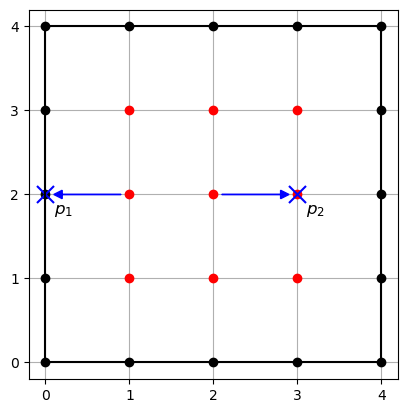
$$ \begin{align*} p_1 + p_2 &= \begin{pmatrix} 1 \\ 2 \\ 5 \end{pmatrix} + \begin{pmatrix} 2 \\ 2 \\ 4 \end{pmatrix} = \begin{pmatrix} 3 \\ 4 \\ 9 \end{pmatrix} \\ &= \begin{pmatrix} 0 \\ 2 \\ 6 \end{pmatrix} + \begin{pmatrix} 3 \\ 2 \\ 3 \end{pmatrix} \\ &\phantom{= \begin{pmatrix} 0 \\ 0 \\ 8 \end{pmatrix} + \begin{pmatrix} 3 \\ 4 \\ 1 \end{pmatrix}} \end{align*} $$
Proof of lemma for $\square^k$¶
- Showing $(R/I_{\square^k})_d = (\overline{R/I_{\square^k}})_d$ for $d \geq 2$ amounts to a computation with the lattice points of $\square^k$.
- We are done if for any $p_1,p_2 \in \overline{\square^k}$, we can write $p_1 + p_2 = q_1 + q_2$ with $q_1,q_2 \in \square^k$.
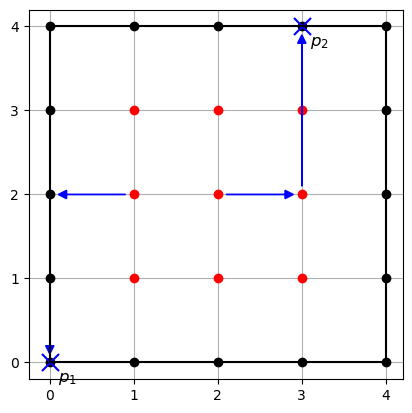
$$ \begin{align*} p_1 + p_2 &= \begin{pmatrix} 1 \\ 2 \\ 5 \end{pmatrix} + \begin{pmatrix} 2 \\ 2 \\ 4 \end{pmatrix} = \begin{pmatrix} 3 \\ 4 \\ 9 \end{pmatrix} \\ &= \begin{pmatrix} 0 \\ 2 \\ 6 \end{pmatrix} + \begin{pmatrix} 3 \\ 2 \\ 3 \end{pmatrix} \\ &= \begin{pmatrix} 0 \\ 0 \\ 8 \end{pmatrix} + \begin{pmatrix} 3 \\ 4 \\ 1 \end{pmatrix} \end{align*} $$
Smooth does not imply $\text{reg}(R/I) = 2$¶
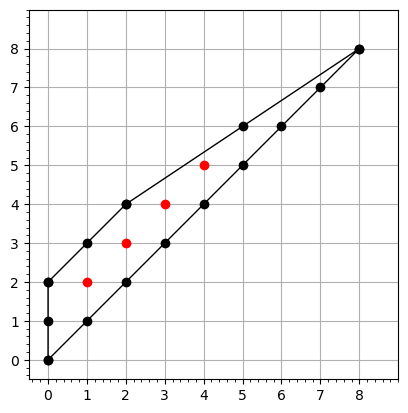
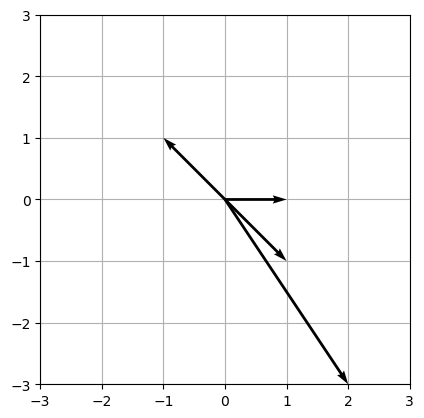
Smooth does not imply $\text{reg}(R/I) = 2$¶
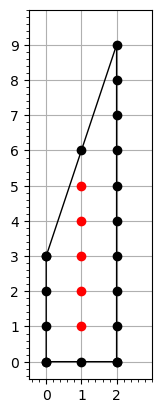
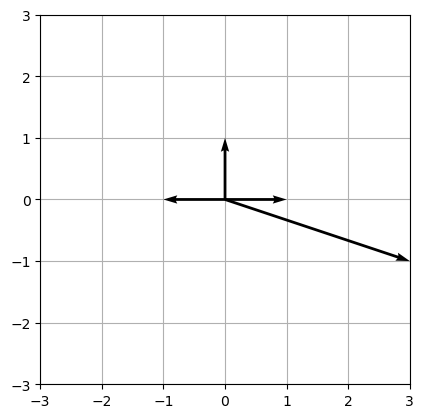
Future work¶
- Conjecture: Suppose $X$ is a smooth toric surface in the setup of the hollow polygons. Let $\Sigma$ be its corresponding fan with rays $\rho_1,\dots,\rho_r$. Then the regularity of $R/I_X$ is bounded by the largest magnitude of a ray of $\Sigma$, i.e., $$\text{reg}(R/I_X) \leq \max_{1 \leq i \leq r} \lvert \lvert \rho_i \rvert \rvert_1.$$ Alternatively, if $v_1,\dots,v_r = v_0$ are the vertices of the corresponding polytope $P$ (ordered clockwise), then $$\text{reg}(R/I_X) \leq \max_{1 \leq i \leq r} \frac{\lvert \lvert v_i - v_{i-1} \rvert \rvert_1}{\gcd(v_i - v_{i-1})}.$$
Other Projects¶
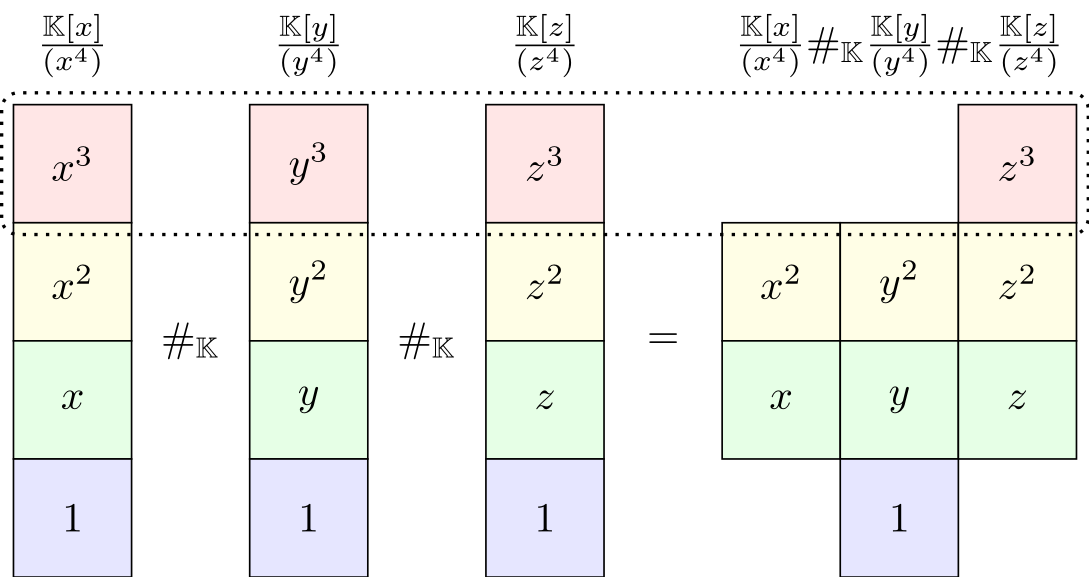
Betti numbers for connected sums of graded Artinian Gorenstein algebras¶
Joint with Nasrin Altafi, Roberta Di Gennaro, Federico Galetto, Rosa M. Mirò-Roig, Uwe Nagel, Alexandra Seceleanu, Junzo Watanabe
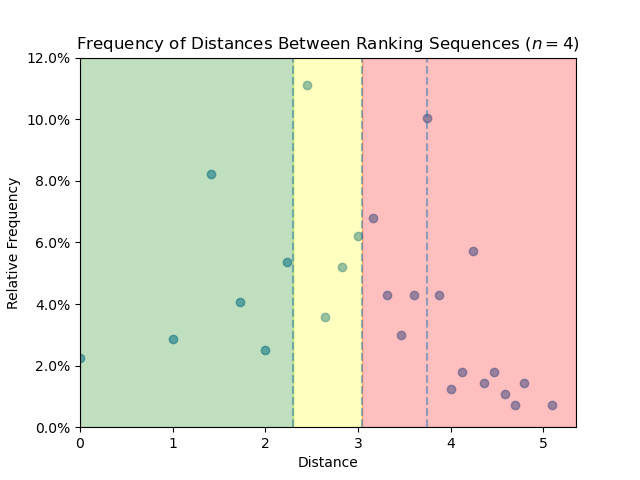
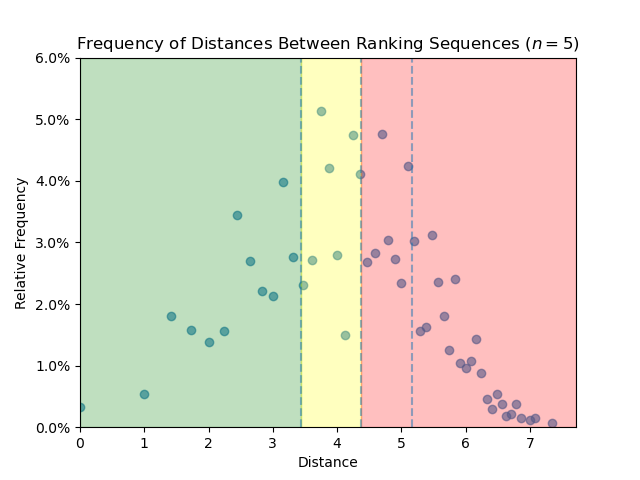
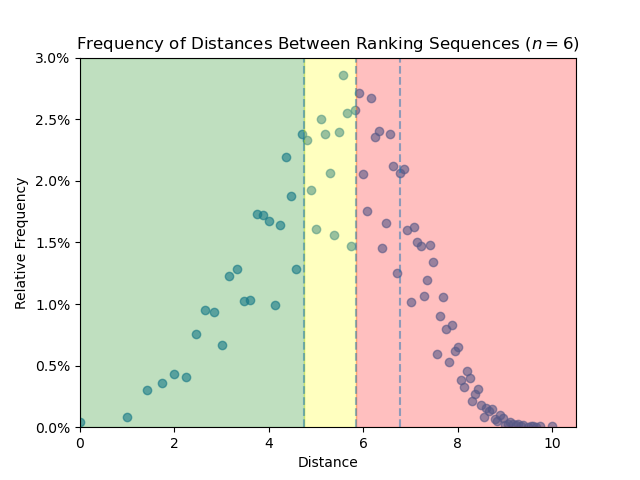
Graph Theoretic Reflection to Foster Alignment in Coordinated Courses¶
Joint with Haile Gilroy and Melinda Lanius
MatrixSchubert package for Macaulay2¶

Joint with Ayah Almousa, Daoji Huang, Patricia Klein, Adam LaClair, Yuyuan Luo, Joseph McDonough
Summary¶
Betti tables forcing failure of the Weak Lefschetz Property (published in Springer INdAM)
Betti numbers for connected sums of graded Gorenstein artinian algebras (published in TAMS)
| The MatrixSchubert package for Macaulay2 (published in JSAG)
Graph Theoretic Reflection to Foster Alignment in Coordinated Course (resubmitted)
Combinatorial bounds on the Castelnuovo-Mumford regularity of toric surfaces (nearing completion)