Definitions

Let \( \leq_T \) denote the stable Tamari order (to be defined at a later date) and \( (\mathbb{N}^n, \leq_T) \) a stable Tamari poset. For any \( \mathbf{a} \in \mathbb{N}^n \), we can represent it as a diagram of black and white boxes separated by a vertical line where the number of white boxes in row \( i \) is \( \mathbf{a}_i \) (counting from top to bottom).

• Definition. Given \( \mathbf{b} \in \mathbb{N}^n \), define the lower order ideal of \( \mathbf{b} \) to be \( \mathbf{b}_\downarrow = \{ \mathbf{a} \in \mathbb{N}^n \, \vert \, \mathbf{a} \leq_T \mathbf{b} \} \).

  

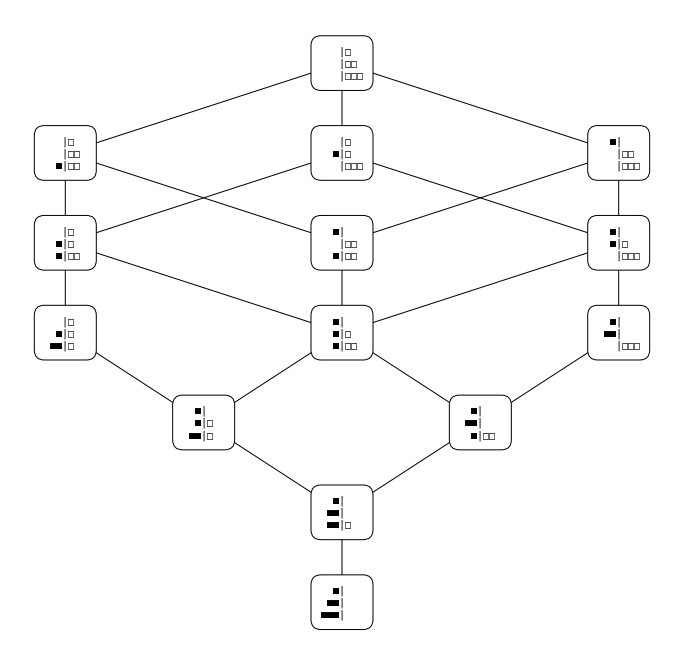
• Definition. Let \( \mathbf{a} \leq_T \mathbf{b} \). The height from \( \mathbf{a} \) to \( \mathbf{b} \) as the maximum length of a chain from \( \mathbf{a} \) to \( \mathbf{b} \) in the stable Tamari poset and is denoted \( \text{ht}(\mathbf{a}, \mathbf{b}) \).
• Definition. Let \( \mathbf{b} \in \mathbb{N}^n \). Define the generating functions \[ f_{\mathbf{b}}(t) = \sum_{\mathbf{a} \in \mathbf{b}_\downarrow} t^{\text{ht}(\mathbf{a}, \mathbf{b})} \quad \text{and} \quad F_{\mathbf{b}}(t) = \sum_{[\mathbf{p}, \mathbf{q}] \subseteq \mathbf{b}_\downarrow} t^{\text{ht}(\mathbf{p}, \mathbf{q})}. \]

Example

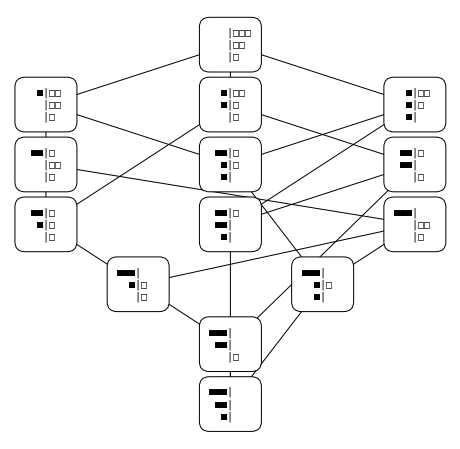
Let \( \mathbf{b} = (3,2,1) \). The Hasse diagram for \( \mathbf{b}_\downarrow \) is shown below. Tracing through the chains in the Hasse diagram, it can be seen that \( \text{ht}((0,0,0), \mathbf{b}) = 6 \) and \( \text{ht}((0,1,0), (2,2,1)) = 3 \). With some computation, it can be shown that \[ \begin{align*} f_{\mathbf{b}}(t) &= t^6 + t^5 + 2t^4 + 3t^3 + 3t^2 + 3t + 1 \\ &\, \\ F_{\mathbf{b}}(t) &= t^6 + 2t^5 + 5t^4 + 10t^3 + 15t^2 + 21t + 14 \end{align*} \]

Catalan connections

Joint with Herman Chau, Spencer Daugherty, Juan Carlos Martínez Mori, and Anna Pun.

To better understand stable Tamari posets, we are interested in determining the possible sizes of lower order ideals, and in particular, finding the minimum size for a fixed \( n \). Restricting to permutations in \( \mathfrak{S}_n \), we conjecture (and supported by computational evidence) that the minimum size of a lower order ideal is given by \( C_{n+1} \), the \( (n+1) \)-st Catalan number. Moreover, it seems like the minimizers are the permutations which are unimodal. While it seems like this characterizes those permutations with the minimum size, we would still like to figure out what feature(s) determines the size of the lower order ideal.

Unimodality

Joint with Herman Chau, Spencer Daugherty, Juan Carlos Martínez Mori, and Anna Pun.

To obtain a finer view of the structure of the lower order ideals, we introduced the \( f_{\mathbf{b}}(t) \) and \( F_{\mathbf{b}}(t) \) generating functions. Again supported by computational evidence, we conjecture that the coefficients of the \( f_{\mathbf{b}}(t) \) generating function and \( F_{\mathbf{b}}(t) \) are unimodal. This would suggest a much richer structure to the lower order ideals than previously thought, and that there might be a combinatorial interpretation for the coefficients. The example above in the Background section shows an example of this phenomenon.